Гидростатика
Гидростатика изучает законы равновесия жидкости. Под равновесием понимается отсутствие перемещения частиц жидкости относительно стенок сосуда и друг друга. При этом если стенки сосуда неподвижны, то говорят об абсолютном равновесии, если сосуд движется, то имеют в виду равновесие жидкости.
Жидкость при этом рассматривается как непрерывная среда, заполняющая пространство полностью без пустот и промежутков.
Вследствие текучести жидкости в ней не могут действовать сосредоточенные силы, а возможно лишь действие сил, непрерывно распределенных по ее объему или по поверхности. Поэтому силы, действующие на рассматриваемые объемы жидкости и являющиеся по отношению к ним внешними силами, подразделяются на массовые и поверхностные.
Массовые силы пропорциональны массе жидкого тела или для однородной жидкости пропорциональны его объему. Это силы тяжести и силы инерции переносного движения.
Поверхностные силы непрерывно распределены по поверхности жидкости и пропорциональны величине этой поверхности.
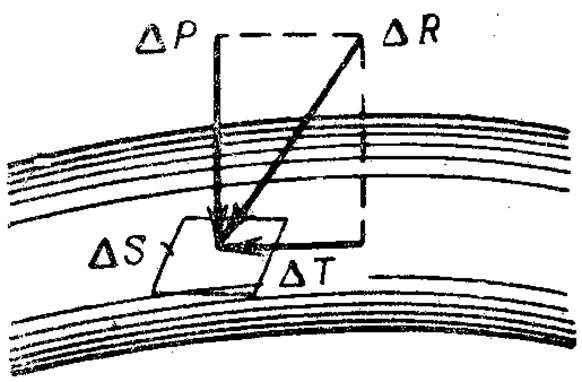
Поверхностная сила 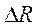 , действующая на площади
, действующая на площади 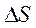 , направлена под некоторым углом к ней и силу
, направлена под некоторым углом к ней и силу 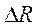 можно разложить на нормальную
можно разложить на нормальную 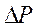 и тангенциальную
и тангенциальную 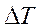 составляющие. Первая направлена внутрь объема и называется силой давления, а вторая силой трения.
составляющие. Первая направлена внутрь объема и называется силой давления, а вторая силой трения.
Выделив некоторую площадь, 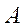 получим следующие определения:
получим следующие определения:
- отношение силы трения к площади поверхности трения называется касательным напряжением трения
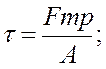
- отношение силы давления к площади поверхности воздействия называется средним гидростатическим давлением
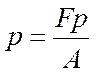
При неограниченном уменьшении площади 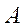 участка поверхности получим соответственно касательное напряжение
участка поверхности получим соответственно касательное напряжение 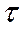 и гидростатическое давление
и гидростатическое давление 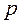 в точке:
в точке:

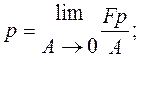
Гидростатическоедавление обладает двумя свойствами:
1. Всегда направлено по нормали внутрь рассматриваемого объема жидкости и является сжимающим.
2. В любой точке покоящейся жидкости не зависит от ориентации площадки, на которую оно действует, т.е. оно действует одинаково по всем направлениям.
Первое свойство доказывается тем, что если бы в покоящейся жидкости была бы касательная составляющая, то она бы вывела жидкость из состояния равновесия и она начала бы двигаться вдоль площадки, т.е. перестала быть неподвижной.
Второе свойство доказывается следующим образом:
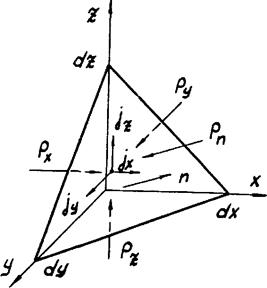
| Выделим в жидкости элементарный объем в виде прямоугольного тетраэдра с произвольными ребрами 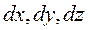 . При этом произвольно наклоненная плоскость тетраэдра имеет . При этом произвольно наклоненная плоскость тетраэдра имеет
|
площадь 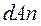 и вдоль ее нормали
и вдоль ее нормали 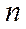 действует давление
действует давление 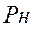 . Сумма массовой и всех поверхностных сил, действующих на выделенный объем равна нулю. В частности, для сил, действующих вдоль оси
. Сумма массовой и всех поверхностных сил, действующих на выделенный объем равна нулю. В частности, для сил, действующих вдоль оси 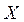
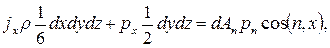
где 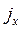 - проекция единичной массовой силы;
- проекция единичной массовой силы;
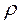 - плотность жидкости.
- плотность жидкости.
Учитывая, что 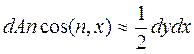 , получим
, получим 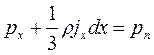 .
.
При уменьшении объема до точки 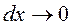 приходим к равенству
приходим к равенству 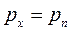 . Аналогично можно получить равенство
. Аналогично можно получить равенство 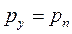 и
и 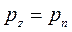 . Таким образом, в любой внутренней точке жидкости гидростатическое давление по всем направлениям одинаково.
. Таким образом, в любой внутренней точке жидкости гидростатическое давление по всем направлениям одинаково.
Дата добавления: 2015-10-13; просмотров: 598;
