Долгосрочные средние издержки

При неизменных ценах на ресурсы эффект масштаба обусловливает динамику издержек в долгосрочном периоде. Ведь именно он показывает, приводит ли наращивание производственных мощностей к уменьшению или увеличению отдачи.

Эффективность использования ресурсов в данном периоде удобно анализировать с помощью функции долгосрочных средних издержек LATC. Что представляет собой эта функция? Предположим, что правительство Москвы решает вопрос о расширении принадлежащего городу завода АЗЛК. При имеющейся производственной мощности минимизация издержек достигается при объеме производства в 100 тысяч автомобилей в год. Это положение вещей отображает кривая краткосрочных средних издержек ATC₁, соответствующая данному масштабу производства (рис. 6.15). Пусть введение новых моделей, выпуск которых намечен совместно с «Рено», увеличило спрос на автомобили. Местный проектный институт предложил два проекта расширения завода, соответствующих двум возможным масштабам производства. Кривые ATC₂ и ATC₃ являются кривыми краткосрочных средних издержек для этих больших масштабов производства. При принятии решения о варианте расширения производства руководство завода, помимо учета финансовых возможностей инвестирования, примет во внимание два основных фактора — величину спроса и значение издержек, с которыми можно произвести требуемый объем производства. Необходимо выбрать масштаб производства, который обеспечит удовлетворение спроса при минимальных издержках на единицу продукции.

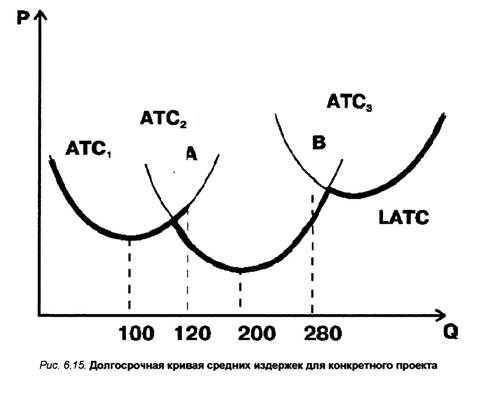
Рис. 6.15. Долгосрочная кривая средних издержек для конкретного проекта

Здесь принципиальное значение имеют точки пересечения соседних кривых краткосрочных средних издержек (точки А и В на рис. 6.15). Сравнением соответствующих этим точкам объемов выработки и величины спроса определяют необходимость наращивания масштаба производства. В нашем примере, если величина спроса не превысит 120 тыс. автомобилей в год, производство целесообразно осуществлять при масштабе, описываемом кривой ATC₁, т.е. на существующих уже мощностях. В этом случае достижимые удельные издержки минимальны. Если спрос возрастет до 280 тыс. автомобилей в год, то наиболее подходящим был бы завод с масштабом производства, описываемым кривой ATC₂. Значит, целесообразно осуществить первый инвестиционный проект. Если же спрос превысит 280 тысяч автомобилей в год, придется реализовывать второй инвестиционный проект, т.е. расширять масштаб производства до размеров, описываемых кривой ATC₃.

В долгосрочном периоде хватит времени для воплощения в жизнь любого возможного инвестиционного проекта. Поэтому в нашем примере кривая долгосрочных средних издержек будет состоять из последовательных участков кривых краткосрочных средних издержек до точек их пересечения со следующей такой кривой (жирная волнообразная линия на рис. 6.15).

Таким образом, каждая точка кривой долгосрочных издержек LATC определяет минимальные достижимые издержки на единицу продукции при данном объеме производства с учетом возможности изменения масштаба производства.

В предельном случае, когда под любую величину спроса строится свой завод соответствующего масштаба, т.е. существует бесконечно много кривых краткосрочных средних издержек, кривая долгосрочных средних издержек из волнообразной видоизменяется в плавную линию, огибающую все кривые краткосрочных средних издержек. Каждая точка кривой LATC является точкой касания с определенной кривой ATC_n (рис. 6.16).

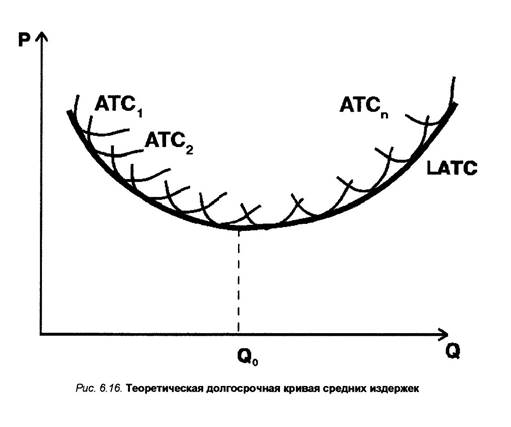
Рис. 6.16. Теоретическая долгосрочная кривая средних издержек