Статистическое изучение взаимосвязей или корреляционно-регрессионный анализ.

Изучение действительности показывает, что вариация каждого изучаемого признака находится в тесной связи и взаимодействии с вариацией других признаков, характеризующей исследуемую совокупность единиц.

Признаки бывают факторными и результативными. Признаки, вызывающие изменения других, связанных с ними, признаков, называются факторными. Признаки, изменяющиеся под действием факторных признаков, называются результативными.

Между факторными и результативными признаками возникают причинно-следственные отношения, проявляющиеся во временной последовательности (причина, затем следствие).

Связи между явлениями и их признаками классифицируются по степени тесноты связи, направлению и аналитическому выражению.

В статистике различают две категории зависимости:

- функциональная;

- корреляционная.

Функциональная зависимость – математическая функция ( ).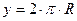

Корреляционная зависимость включает случайные факторы.

Характерное свойство корреляционных связей:

1. Они применяются не в единичных случаях, а требуют для своего исследования массовых наблюдений.

2. Корреляционные связи являются неполными, поэтому даже на массовом материале, где случайные факторы сглаживаются, зависимости не будут носить полного характера, т.е. функционального характера.

В статистике принято различать следующие виды корреляционных зависимостей:

1. Парная корреляция.

Связь между двумя признаками – результативным и факторным или двумя результативными.

2. Частная корреляция.

Зависимость между результативными и одним факторным признаком при фиксированном значении других факторных признаков.

3. Множественная корреляция.

Зависимость результативного и двух или более факторных признаков, включающих исследуемые.

При многофакторной связи считается, что все факторы действуют комплексно, т.е. одновременно и во взаимосвязи.

Задача корреляционного анализа состоит в определении тесноты связи между результативным и факторным признаками.

Теснота связи характеризуется коэффициентом корреляции, а форма связи исследуется с помощью регрессии.

Регрессия может быть однофакторной, т.е. парной, и многофакторной, т.е. множественной. По форме связи могут быть прямолинейными и криволинейными.

Прямолинейная связь выражается уравнением прямой, а график – прямая линия.

При криволинейной связи наблюдается возрастание или убывание величины результативного признака при возрастании факторного признака.

Геометрически такие связи выражаются гиперболами, параболами и др. математическими функциями.