Все элементы системы имеют основное (последовательное) соединение
Выше указывалось, что основным или последовательным соединением считается (в, смысле надежности) такое, когда отказ одного из элементов приводит к отказу всей системы в целом. Данный случай является самым простым и самым важным.
Для безотказной работы системы в течение времени t нужно, чтобы каждый элемент работал безотказно в течение этого же времени. Так как элементы независимы в смысле надежности, то функции надежности элементов перемножаются
Р(t)=р1(t)× р2(t)...pn(t), (3.42)
или
P(t)=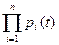 
. (3.43)
Выразим функции надежности через интенсивности отказов
l(t)= l1(t)+ l2(t)+...+ ln(t). (3.44)
При основном (последовательном) соединении элементов интенсивности отказов складываются. В частности, для экспоненциального закона, когда lк(t)=lк = const,
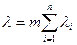(3.45)
тогда
Р(t)=exp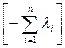 
t. (3.46)
Если надежность элементов подчиняется экспоненциальному закону, то надежность системы также будет подчиняться экспоненциальному закону.
Обозначим Т0—среднее время жизни системы, а через Tк— среднее время жизни К-того элемента.
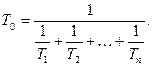(3.47)
В сложной системе всегда могут быть группы одинаковых элементов, выполняющих одинаковые функции, надежности которых можно принять одинаковыми. Для них формулы (3.42) и (3.43) запишутся так
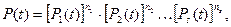(3.48)
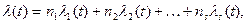(3.49)
где пi — число элементов в группе от 1 до s.
Для экспоненциального закона
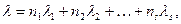(3.50)
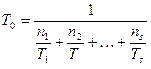(3.51)
В частном случае, когда все элементы имеют одинаковую надежность рк(t)=р(t)
Р(t)=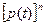 
(3.52)
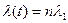(t), (3.53)
для экспоненциального закона
l=пli, (3.54)
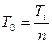. (3.55)
Определим вероятность отказа:
Q(t)=1-P(t) qк(t)=1-Pк(t).
Тогда для основного (последовательного) соединения
Q(t)=1-[1-q1(t)][1-q2(t)]…[1-qn(t)]; (3.56)
Q(t)=1-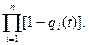 
Если выполняется условие
q1(t)+q2(t)+…+qn(t)<<1,
то можно пользоваться приближенной формулой
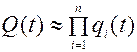(3.56)
В этом случае величина погрешности не превосходит
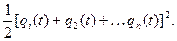
Дата добавления: 2015-10-05; просмотров: 804;