Химизм Земли

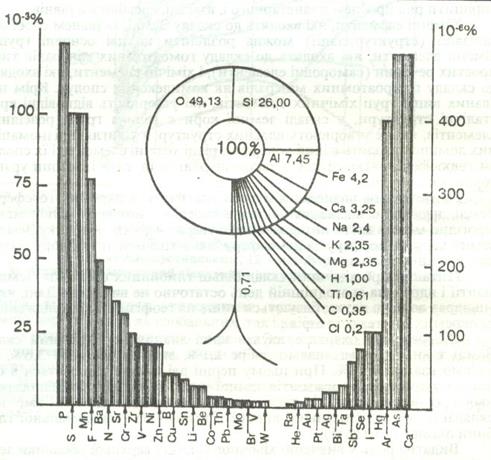
Для определения химического состава Земли и ее оболочек используют данные о метеоритах, представляющих собой наиболее вероятные образцы протопланетного материала, из которого сформировались планеты земной группы и астероиды. Среднее содержание химического элемента в земной коре называется кларком (по имени американского ученого Ф. Кларка, начавшего изучение состава земной коры в конце XIX ст.). Он выражается в весовых, объемных или атомных процентах. На долю O + Si + Al + Fe + Ca + Mg приходится 94,14 % (рис. 5).

Особенности распространения элементов: 1) наиболее распространены от H до Zn (1-30); 2) кларки четных элементов больше нечетных (четные 86,4%); 3) из четных наиболее распространены отличающиеся разностью порядковых номеров 6 (O - 8; Si – 14; Ca – 20; Fe – 26…).

Химический состав земной коры изменяется во времени: 1) поступление метеоритного вещества; 2) рассеивание легких газов (H и He) в мировое пространство; 3) распад радиоактивных элементов; 4) перемещение химических элементов из одной оболочки в другую (вулканы и землетрясения) и др.

На основании анализа состава различных метеоритов, а также сведений, полученных в результате экспериментальных геохимических и геофизических данных и термодинамических расчетов. Повышенное распространение характерно только для четырех элементов — О, Fe, Si, Мg, в сумме составляющих 91 %. В группу менее распространенных элементов входят Ni, S, Са, А1.

КРИСТАЛОГРАФІЯ

1.1 ПРЕДМЕТ КРИСТАЛОГРАФІЯ

Земна кора складається з кристалічної речовини на 95%. Метали, сплави, кераміка, бетон, фарфор, тверді шлаки мають кристалічну будову.

Кристаллография – наука о процессах образования, форме, структуре и физико-механических свойствах кристаллов. Перед кристаллографией стоят практические задачи: изучение образования, строения и свойств кристаллов реальной среды, получение искусственных кристаллов. Синтетические кристаллы реальной среды широко применяются в приборостроении, ювелирной промышленности, радиотехнике, оптике, акустике и т. д., состоит из следующих разделов:

1. Геометрическая – изучает внешнюю форму и симметрию кристаллов, геометрические законы кристаллографии.

2. Химическая – о внутреннем строении кристаллических веществ и их зависимости от химического состава.

3. Физическая – о физических свойствах кристаллов (механические, оптические, тепловые, электрические, магнитные и т.д.).

Кристаллы – твёрдые тела формы многогранника, с закономерным расположением в пространстве элементарных частиц (атомы, ионы, молекулы). Различают кристаллы природные и синтетические, полученные искусственным путём. Искусственные кристаллы – кристаллы, не имеющих аналогов в природе ввиду существующих определённых геохимических ассоциаций химических элементов и величины их концентрации.

Аморфное вещество характеризуется отсутствием кристаллического строения, физические свойства одинаковы во всех направлениях (стекло, газ, жидкость), вследствие хаотичного расположения атомов.

Свойства кристаллических веществ обусловлены их внутренним строением:

1. Однородность – свойство физического тела быть одинаковым во всём объёме. Свойства на разных участках кристалла в параллельных направлениях одинаковы (кристаллы кубической сингонии).

2. Анизотропия (неравносвойственность) – свойства различны в непараллельных направлен так как различны расстояния между материальными частицами (механические свойства слюды, графита, дистена).

3. Дискретность внутреннего строения – свойства кристалла не могут быть одинаковы там, где есть частицы и где их нет.

4. Способность самоограняться свойства кристаллов быть образовывать грани при свободном их росте. Если шарик галита поместить в пересыщенный раствор хлорида натрия, то этот шарик в конце концов обрастёт гранями куба.

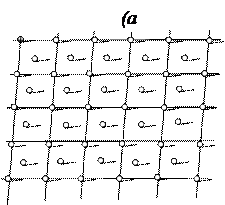
Металлы в аморфном состоянии обладают специфическими свойствами, прежде всего тягучестью и пластичностью, что позволяет изготовлять из него головки магнитной записи, бритвы лезвия, получать металлическую фольгу толщиной 10мкм и проволоку диаметром 10мкм. Промежуточными звеньями между аморфным и кристаллическим состоянием вещества являются полимеры и жидкие кристаллы (рис.1). Мономерные цепи полимеров состоят из закономерно повторяющихся частиц, тогда как взаимное расположение этих цепей друг относительно друга может быть различным, так как связи между ними слабые и поэтому возможно проскальзывание этих цепей друг относительно друга. Жидкие кристаллы представляют собой жидкость, состоящую из вытянутых молекул, способных приобретать определённую ориентировку друг относительно друга под действием внешнего электрического поля. Таким образом и полимеры и жидкие кристаллы обладают лишь частично упорядоченным строением. Кристаллическое стекло – ситал более прочное по сравнению с аморфным стеклом.

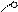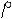Рис.1 – Двумерная схема расположения материальных частиц в кристаллах (а), полимерах (б), жидких кристаллах (в) и аморфных телах (г).

1.2.1 Просторові решітки

Геометрическая кристаллография – раздел кристаллографии, который изучает законы симметрии, формы кристаллов и их сочетаний, законы срастаний кристаллов.

Пространственная решётка

Мельчайшие частички любого кристаллического вещества закономерно располагаются в пространстве, образуя правильные ряды, которые в трёхмерном пространстве образуют кристаллическую решётку. Частицы колеблются около узлов кристаллической решётки. Узлы кристаллической решётки, лежащие вдоль прямой, образуют ряд решётки, а расстояние между ближайшими узлами а – промежуток ряда. Плоская сетка – совокупность частиц, лежащих в одной плоскости в вершинах системы равных параллелограммов параллельных и смежных по сторонам. Два ряда ОА_n и ОВ_n задают плоскую сетку (Рис. ). Возьмём узел С₁, расположенный вне плоскости сетки и проведём ряд О-С₁-С₂… и плоские сетки, в результате чего получим пространственную решётку (Рис. 1.2).

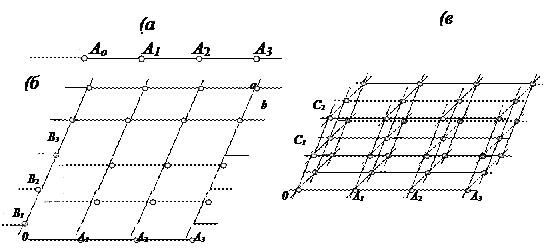Рисунок 1.2 – Просторові решітки (с) і їх елементи: одномірний ряд (а) і плоска сітка (б)

Пространственная решётка – система точек, расположенных в вершинах равных, параллельно ориентированных параллелепипедов без промежутка заполняющих пространство. Эти параллелепипеды называют элементарной ячейкой (рис. 1.3). Форма ячейки зависит от её параметров а, в, с и углов между ними α, β, γ. Так, для кубиков галита а=в=с, а α=β=γ=90⁰.

Грань – плоскость, ограничивающая кристалл. Ребро – линия пересечения граней. Вершина – точка пересечения рёбер.

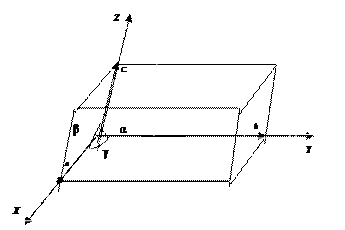Рисунок 1.3 – Элементарная ячейка

2.2.4Симметрия кристаллов.

Симметрия (соразмерность) – способность кристалла закономерно повторять свои части в пространстве.

Симметричная фигура состоит из равных, правильно повторяющихся частей и может совмещаться сама с собой в результате симметричных преобразований (отражение, вращение, перенос).

Элементы симметрии – точки, прямые, плоскости, относительно которых закономерно повторяются части симметричных фигур.

Ось симметрии – пряма, вращая вокруг которой фигура совмещается. Ось симметрии обозначается в виде знака «L_n», где n – число самосовмещений кристалла при его повороте на 360⁰, которое называется порядком оси (2, 3, 4, 6). Число осей обозначается в виде цифры перед буквой оси - 3L₄, 4L₃. Для оси L₂ самосовмещение наступает через 180⁰, для оси L₃ – через 120⁰, L₄ – через 90⁰, L₆ – через 60⁰. Правильное расположение узлов кристаллической решётки не допускает существования осей других порядков (рис.2.6). Оси симметрии проходят через центр граней, середину рёбер и вершины.

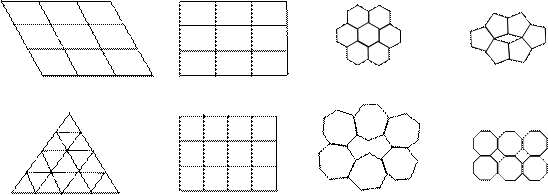Рисунок 2.6 – Плоские сетки, составленные из многогранников с осями симметрии 1-8 порядков

Инверсионная ось – сложная ось, так как предполагает две операции: поворот с последующим отражением в центральной точке фигуры, что совместно приводит к самосовмещению фигуры (рис. 2.7). Существуют оси Li₃, Li₄, L_i6, которые имеют эквиваленты: L_i3=L₃C, L_i4=L₂, L_i6=L₃P.

Рисунок 2.7 – Многогранники с инверсионными осями сиимметрии четвёртого (а) и шестого (б) порядка

Існують осі L_і3, L_і4, L_i6, що мають еквіваленти: L_i3=L₃C, L_i4=L₂, L_i6=L₃P.

Центр симметрии (С) – точка внутри кристалла, при проведении через которую любая прямая встретит на равном от неё расстоянии одинаковые обратно расположенные части фигуры.

Плоскость симметрии (Р) – воображаемая плоскость, разделяющая кристалл на две зеркально-отраженные части. Количество плоскостей обозначается в виде числа, стоящего перед буквой Р и может принимать следующие значения: 1 (не пишется), 2, 3, 4, 5, 6, 7, 9. Плоскость Р проходит через С, середину граней и рёбер, перпендикулярно к ним, параллельно рёбрам.

Возможно только 32 комбинации различных группировок элементов симметрии (32 вида симметрии, табл. 2.1).

Единичное направление единственное, не повторяющееся направление в кристалле. Так, в кристаллах кубической сингонии таких направлений нет, в кристаллах средней категории одно (L₃, L₄, L₆), низшей категории – несколько.

Симметрично-равные направления – повторяющиеся направления, связанные элементами симметрии (например 3L₄ у куба или октаэдра).

Сингония – группа видов симметрии, обладающих несколькими сходными элементами симметрии при одинаковом числе единичных направлений.

Категория – сингонии, сходные по симметрии и числу единичных направлений.

КРИСТАЛЛОГРАФИЧЕСКИЕ ОСИ. ПАРАМЕТРЫ. СИМВОЛЫ.

При описании кристаллов необходимо определить положение в пространстве отдельных его граней. Для решения этой задачи за основу берутся оси координат, относительно которых определяем положение граней. Для этого мысленно внутри кристалла проводим кристаллографические оси, пересекающиеся в центре и совпадающие с элементами симметрии, или перпендикулярны к Р, или параллельны рёбрам.

Кристаллографические оси – отрезки координатных осей внутри кристалла, разбивающим пространство на 8 октантов. Ось направленная к наблюдателю – I (X), параллельная наблюдателю - II (Y), вертикальная – III (Z).

Таблиця 1.1 – 32 види симетрії	Вид симетрії	інверсійно-планальний					Lі4(≡L2)2L22Р	Lі63L23Р(=L33L24Р)
інверсійно-примітивний					Lі4(≡L2)	Lі6(=L3Р)
планаксіальний		L2РС	3L23РС		L44L25РС	L66L27РС	3L44L39РС
аксіальний		L2	3L2	L33L23РС	L44L2	L66L2	3L44L36L2
планаль-ний		Р	L22Р	L33L2	L44Р	L66Р	3L44L36Р
централь-ний	С			L33Р	L4РС	L6РС	3L24L3РС
примітив-ний	-			L3	L4	L6	3L24L3
Сингонії	Триклінна	Моноклінна	Ромбічна	Тригональна	Тетрагональна	Гексагональна	Кубічна
Категорії	Нижча	Середня	Вища

Если проводится 4 оси (тригональная и гексагональная сингонии), то III (U), IY (Z). Концы осей, направленные к наблюдателю, вправо и вниз – положительные. Угол a - между осями Z и Y, угол b - между осями Z и X, угол g - между осями X и Y (рис. 2.8).

Каждая сингония имеет свою систему координат и характеризуется своим элементарным параллелепипедом.

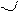
Рисунок 2.8 – Координационные оси всех сингоний

Низшая категория (а¹в¹с) – 53% природных кристаллов.

Триклинная сингония: a¹b¹g¹90⁰, косоугольная система координат, состоит из двух классов: а) С, б) без С.

Моноклинная сингония: a=g=90⁰, b¹90⁰, ось Z^Y, содержит три класса. Ось X наклонена к оси Z. За оси координат принимают рёбра (X, Z), за ось Y – L₂, либо перпендикуляр к Р.

Ромбическая сингония: a=b=g, характерный элемент 3L₂, содержит три класса, за координатные оси принимаются 3L₂, L₂ и перпендикуляр к Р.

Средняя категория(а=в¹с) – 26% природных кристаллов.

Тригональная сингония: a=b=90⁰, g=120⁰, горизонтальные оси равны. За ось Z принимается L₃. Оси Х и Y совмещают с 3L₂, перпендикулярами к Р, либо с рёбрами.

Тетрагональная сингония: a=b=g=90⁰, горизонтальные оси равны между собой. За ось Z принимается L₄, за X и Y – оси L₂.

Гексагональная сингония: a=b=90⁰, g=120⁰, горизонтальные оси равны. За ось Z принимается L₆. Оси Х и Y совмещают с 3L₂, перпендикулярами к Р, либо с рёбрами.

Высшая категория(а=в=с) – 20% природных кристаллов.

Кубическая сингония: a=b=g=90⁰. За оси координат выбираются 3L_4.

За своєю зовнішньою формою усі кристали розподіляються на дві групи: прості форми і складні.

1.2.6 Прості форми кристалів

За своєю зовнішньою формою усі кристали розподіляються на дві групи: прості форми і складні.

Прості форми – многогранники, які складаються з однакових симетрично розташованих граней. Наприклад, куб, октаедр, ромбоедр.

Прості форми можуть повністю замикати простір - закриті форми, а також можуть бути відкритими, які не замикають простір з усіх сторін. Кількість типів простих форм, які входять у різні кристалографічні комбінації, є строго обмеженим і дорівнює 47 (рис. 1.9). Для їх позначення застосовують наступну термінологію з грецької мови: моно –один; ді – два; три – три; тетра – чотири; пента – п'ять; гекса – шість; окта – вісім; додека – дванадцять; едра – грань; гоніа – кут; пінакс – дошка; клiно – нахиляю; син – схожий; трапеца – різнобічний чотирикутник; скалена – різнобічний трикутник.

До відкритих простих форм відносяться: моноедр – форма складена однією гранню; діедр – форма складена з двох граней, які перетинаються; пінакоїд – форма складена з двох паралельних граней; піраміди - форми, складені трьома або більше гранями, які перетинаються в одній точці; призми – форми складені трьома або більше гранями, які перетинаються по паралельних ребрах.

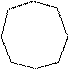
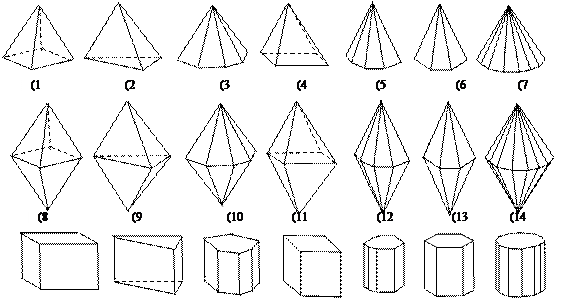
Рисунок 1.9 – Прості форми кристалів:

1–ромбічна піраміда; 2–тригональна піраміда; 3–дітригональна піраміда; 4-тетрагональна піраміда; 5-дітетрагональна піраміда; 6-гексагональна піраміда; 7-дігексагональна піраміда; 8-ромбічна діпіраміда; 9-тригональна діпіраміда; 10-дітригональна діпіраміда; 11-тетрагональна діпіраміда; 12-дітетрагональна діпіраміда; 13-гексагональна діпіраміда; 14-дігексагональна діпіраміда; 15-ромбічна призма; 16-тригональна призма; 17-дітриго-нальна призма; 18-тетрагональна призма; 19-дітетрагональна призма; 20-гексагональна призма; 21- дігексагональна призма; 22 ромбічний тетраедр; 23- тетрагональний тетраедр; 24-тетраедр; 25-тригональний трапецоедр; 26- гексагональний трапецоед; 27- ромбоедр; 28- тетрагональний трапецоедр; 29- куб; 30- октаедр; гексагональний трапецоедр; 31- діедр; 32-пінакоїд; 33- тетрагональний скаленоедр; 34 - моноед; 35- дітригональний скаленоед; 36-тригонтритетраедр; 37-тетрагонтритетраедр; 38-пентагонтритетраедр; 39-ромбододекаедр; 40-пентагондодекаедр; 41-тетрагексаедр; 42-гексатетраедр; 43-ді-додекаедр; 44-тетрагонтриоктаедр; 45-тригонтриоктаедр; 46-пентагонтриоктаедр; 47-гексоктаедр.

До закритих простих форм відносяться: діпіраміди – являють собою дві однакові піраміди, складені своїми основами; скаленоедри – складені різнобічними трикутниками, довжина ребер середнього пояса однакова, вони не лежать в одній площині; трапецоедри – форми, складені різнобічними чотирикутниками, довжина ребер середнього пояса не однакова, вони не лежать в одній площині; ромбоедр – форма, грані котрої мають форму ромбів, являють собою деформований уздовж осі L₃ куб; тетраедри – форми, складені з чотирьох трикутних непаралельних граней. Крім того, до кубічної сингонії відносяться наступні форми: куб (гексаедр) – форма, складена із шести квадратних граней; октаедр – форма, складена з восьми рівнобічних трикутних граней; тетраедр – форма, складена з чотирьох рівнобічних трикутних граней; тригонтритетраедр – похідна форма від тетраедра (на кожній грані тетраедра по три грані у вигляді рівнобедреного трикутника); тетрагонтритетраедр – похідна форма від тетраедра (на кожній грані тетраедра - по три неправильних чотирикутники); пентагонтритетраедр - – похідна форма від тетраедра (на кожній грані тетраедра по три п'ятикутника); ромбододекаедр – форма складена з 12 граней у вигляді ромба; пентагондодекаедр – форма складена з 12 п'ятикутників; гексатетраедр - похідна форма від тетраедра (на кожній грані тетраедра по 6 рівнобедрених трикутника); тетрагексаедр – похідна форма від куба (на кожній грані куба по чотири рівнобедрених трикутники); дидодекаедр – двадцятичотирикутник, який утворюється після розщеплення навпіл граней пентагондодекаедра; тригонтриоктаедр – похідна форма від октаедра (на кожній грані октаедра розташовані по три рівнобедрені трикутника); тетрагонтриоктаедр - похідна форма від октаедра (на кожній грані октаедра розташовані три неправильних чотирикутника); пентагонтриоктаедр - похідна форма від октаедра (на кожній грані октаедра по три рівнобедрені трикутника); гексоктаедр – сорокавісьмикутник (на кожній грані октаедра розташовано по 6 трикутників).

Назви простих форм кубічної сингонії дані по принципу: перша частина слова (тригон, тетрагон, пентагон) характеризує форму грані даної простої форми, друга частина слова вказує, від якої простої форми дана форма є похідною, скільки граней даної простої форми розташовані на кожній грані материнської форми, яка кількість граней даної форми.

Складні форми – являють собою комбінацію в одному кристалі декількох простих форм. Прикладом такої комбінації може бути трикутна тригональна піраміда, яка являє собою комбінацію шести нахилених пірамідальних граней і основи піраміди, яка називається моноедром.

2.7 Законы геометрической кристаллографии. Параметры. Символы

Закон постоянства гранных углов – углы между соответствующими гранями и рёбрами всех кристаллов одного вещества одинаковы (рис.2.10). По двугранным углам, замеряемым при помощи гониометра, выполняется диагностика кристаллов.

Рисунок 2.10 – Кристаллы кварца с различным развитием граней

Плоскость Р отсекает на координатных осях отрезки: по оси Х – а, по оси Y – в, по оси Z – с, которые называются параметрами (рис. 2.11). То есть параметры – отрезки кристаллографических осей, отсекаемые гранью.

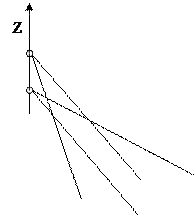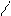
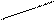
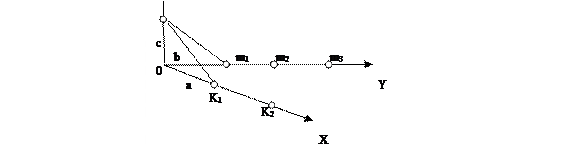
Рисунок 2.11 – К пояснению закона Гаюи

Единичная грань – грань сравнения (а, в, с).

Определяемая грань – сравнимая с единичной (А₁, В₁, С₁). Отношения параметров единичной и определяемой грани выражаются целыми числами: а/А₁=h – индекс по оси Х(I); в/В₁=k – по оси Y(II), с/С₁=l – по оси Z (III).

Индекс – отношение параметров единичной грани к параметрам определяемой грани (индексы Миллера).

Символ – совокупность индексов (hkl).

Так, если параметры единичной грани а=1; в=1; с=1 (Рис. ), а параметры определяемой грани а=0,5; в=0,5; с=2, то символ определяемой грани: (1/0,5:1/0,5:1/2)® (4/2:4/2:1/2)®(441).

Закон Гаюи (двойных рациональных отношений параметров граней) – для любых двух граней кристалла двойные отношения параметров граней равны отношению целых сравнительно малых чисел.