Int x, i, j, temp;

if ( from >= to ) return; // условие окончания рекурсии

i = from; // рассматриваем элементы с A[from] до A[to]

j = to;

x = A[(from+to)/2]; // выбралисреднийэлемент

while ( i <= j ) {

while ( A[i] < x ) i ++; // ищем пару для перестановки

while ( A[j] > x ) j --;

if ( i <= j ) {

temp = A[i]; A[i] = A[j]; A[j] = temp; // перестановка

i ++; // двигаемсядальше

J --;

}

}

QuickSort ( A, from, j ); // сортируемлевуючасть

QuickSort ( A, i, to ); // сортируем правую часть

}

Насколько эффективна такая сортировка? Все описанные ранее способы сортировки массивов имели порядок O(n2), то есть при увеличении в 10 раз длины массива время сортировки увеличивается в 100 раз. Можно показать, что Quicksort имеет в среднем порядок O(n·log n), что значительно лучше.

Чтобы почувствовать, что такое O(n·log n)и O(n2), посмотрите на таблицу, где приведены числа, иллюстрирующие скорость роста для нескольких разных функций.

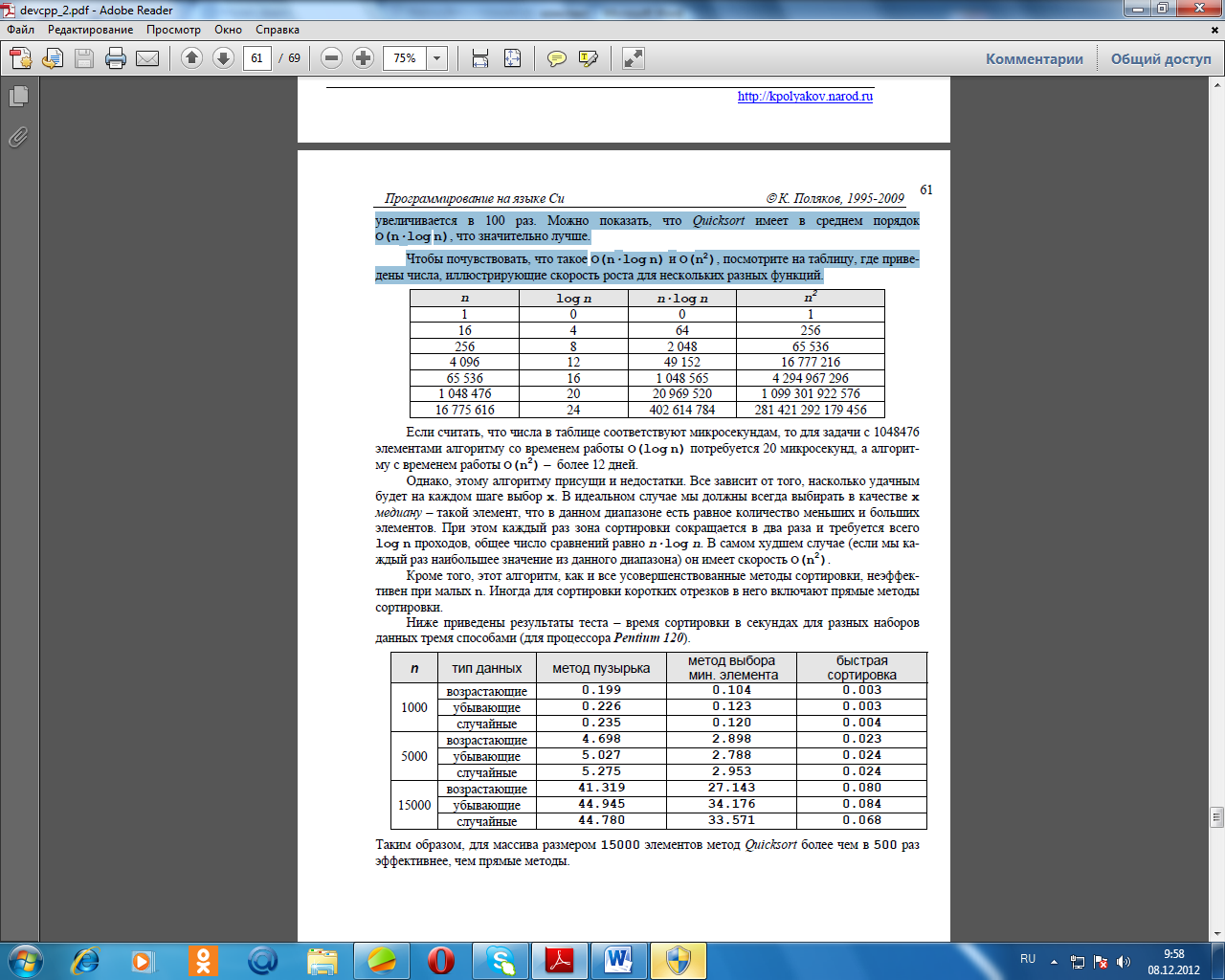
Если считать, что числа в таблице соответствуют микросекундам, то для задачи с 1048476

элементами алгоритму со временем работы O(log n)потребуется 20 микросекунд, а алгоритму с временем работы O(n2)– более 12 дней.Однако, этому алгоритму присущи и недостатки. Все зависит от того, насколько удачным будет на каждом шаге выбор x. В идеальном случае мы должны всегда выбирать в качестве xмедиану – такой элемент, что в данном диапазоне есть равное количество меньших и больших элементов. При этом каждый раз зона сортировки сокращается в два раза и требуется всего log nпроходов, общее число сравнений равно n·log n. В самом худшем случае (если мы каждый раз наибольшее значение из данного диапазона) он имеет скорость O(n2).

Кроме того, этот алгоритм, как и все усовершенствованные методы сортировки, неэффективен при малых n. Иногда для сортировки коротких отрезков в него включают прямые методы сортировки.Ниже приведены результаты теста – время сортировки в секундах для разных наборов данных тремя способами (для процессора Pentium 120).

Таким образом, для массива размером 15000элементов метод Quicksort более чем в 500раз эффективнее, чем прямые методы.