Взаимодействие УУ и АЛУ
Революционность идей фон Неймана заключалась в специализации: каждое устройство отвечает за выполнение только своих функций. Если раньше, например, память часто не только хранила данные, но и могла производить операции над ними, то теперь было предложено, чтобы память только хранила данные, АЛУ производило арифметико-логические операции над ними, устройство ввода только вводило данные из ²внешнего мира² в память и т.д. Фон Нейман распределил функции между различными устройствами, что существенно упростило схему машины.
Устройство управления тоже имеет свои регистры, оно может считывать команды из памяти на специальный регистр команд (RK), на котором всегда хранится текущая выполняемая команда. Регистр УУ с именем RA называется счётчиком адреса, при выполнении текущей команды в него записывается адрес следующей команды (первую букву в сокращении слова регистр будем записывать латинской буквой R).
Рассмотрим, например, операцию сложения двух чисел z:=x+y (здесь x, y и z – адреса ячеек памяти, в которых хранятся, соответственно, операнды и результат сложения). При получении такой команды УУ последовательно посылает управляющие сигналы в АЛУ, предписывая ему сначала считать операнды x и y из памяти и поместить их на регистры R1 и R2. Затем по следующему управляющему сигналу АЛУ производит операцию сложения чисел на регистрах R1 и R2 и записывает результат на регистр S. По следующему управляющему сигналу АЛУ пересылает копию регистра S в ячейку памяти с адресом z. Ниже приведена иллюстрация описанного примера на языке Паскаль, где R1, R2 и S – регистры АЛУ, ПАМ – массив, условно обозначающий память ЭВМ, а Ä – операция (в нашем случае это сложение, т.е. Ä = +).
R1:=ПАМ[x]; R2:=ПАМ[y]; S:=R1ÄR2; ПАМ[z]:=S;
В дальнейшем конструкция ПАМ[А] для краткости будет обозначаться как <А>, тогда наш пример перепишется так:
R1:=<x>; R2:=<y>; S:=R1ÄR2; <z>:=S;
Опишем теперь более формально шаги выполнения одной команды в машине фон Неймана:
RK:=<RA>; считать из памяти очередную команду на регистр команд;
RA:=RA+1; увеличить счётчик адреса на единицу;
Выполнить очередную команду.
Затем выполняется следующая команда и т.д. Итак, если машинное слово попадает на регистр команд, то оно интерпретируется УУ как команда, а если слово попадает в АЛУ, то оно по определению считается числом. Это позволяет, например, складывать команды программы как числа, либо выполнить некоторое число как команду. Разумеется, обычно такая ситуация является семантической ошибкой, если только специально не предусмотрена программистом для каких-то целей (мы иногда будем оперировать с командами, как с числами, в нашей учебной машине).
Современные ЭВМ в той или иной степени нарушают все принципы фон Неймана. Например, существуют компьютеры, которые различают команды и данные. В них каждая ячейка памяти кроме собственно машинного слова содержит ещё специальный признак, называемый тэгом, который и определяет, чем является машинное слово. В этой архитектуре при попытке выполнить число как команду, либо складывать команды как числа, будет зафиксирована ошибка. Так нарушается принцип неразличимости команд и чисел.
Практически все современные ЭВМ нарушают принцип однородности и линейности памяти. Память может быть, например, двумерной, когда адрес ячейки задаётся не одним, а двумя числами, либо ячейки памяти могут вообще не иметь адресов (такая память называется ассоциативной) и т.д.
Достаточно мощные компьютеры нарушают и принцип последовательного выполнения команд: они одновременно могут выполнять несколько команд как из одной программы, так, иногда, и из разных программ (такие компьютеры могут иметь несколько центральных процессоров, а также быть так называемыми конвейерными ЭВМ, их мы рассмотрим в конце нашего курса).
Особо следует отметить, что в архитектуре машины фон Неймана реализованы и другие принципы, которые самим фон Нейманом явно не формулировались, так как считались самоочевидными. Так, например, предполагается, что во время выполнения программы не меняется число узлов компьютера и взаимосвязи между ними. В то же время сейчас существуют ЭВМ, которые нарушают и этот принцип. Во время работы одни устройства могут, как говорят, отбраковываться (например, отключаться для ремонта), другие – автоматически подключаться, появляются новые связи между элементами ЭВМ (например, в так называемых транспьютерах) и т.д.
На этом мы закончим краткое описание машины фон Неймана и принципов её работы. И в заключение этого раздела мы совсем немного рассмотрим архитектуру ЭВМ на уровне инженера-конструктора. Это будет сделано исключительно для того, чтобы снять тот покров таинственности с работы центрального процессора, который есть сейчас у некоторых студентов: как же машины может выполнять различные операции, неужели она такая умная?
Аппаратура современных ЭВМ состоит из некоторых элементарных конструктивных элементов, называемых вентилями. Каждый вентиль реализует одну из логических операций, у него есть один или два входа и один выход. На входах и выходе могут быть электрические сигналы двух видов: низкое напряжения (трактуется как ноль или логическое значение false) и высокое (ему соответствует единица или логическое значение true). Основные вентили следующие.
1. Отрицание, этот вентиль имеет один вход и один выход, если на входе значение true, то на выходе значение false и наоборот. Будем изображать этот вентиль так:
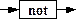
2. Дизъюнкция или логическое сложение, реализует хорошо известную Вам операцию Паскаля or, будем изображать его как 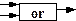
3. И, наконец, конъюнкция или логическое умножение, изображаемое как
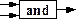
Каждый вентиль срабатывает (т.е. преобразует входные сигналы в выходные) не непрерывно, а только тогда, когда на вентиль по специальному управляющему проводу приходит так называемый тактовый импульс. Заметим, что по этому принципу работают ЭВМ, которые называются дискретными, в отличие от аналоговых компьютеров, схемы в которых работают непрерывно. Подавляющее число современных ЭВМ являются дискретными, только их мы и будем изучать. Более подробно об этом можно прочесть в книгах [1,3].
Из вентилей строятся так называемые интегральные схемы – это набор вентилей, соединённых проводами и такими радиотехническими элементами, как сопротивления, конденсаторы и индуктивности. Каждая интегральная схема тоже имеет свои входы и выходы и реализует какую-нибудь функцию узла компьютера. В специальной литературе интегральные схемы, которые содержат порядка 1000 вентилей, называются малыми интегральными схемами (МИС), порядка 10000 вентилей – средними (СИС), порядка 100000 – большими (БИС) и более 100000 вентилей – сверхбольшими интегральными схемами (СБИС).
Большинство современных интегральных схем собираются на одной небольшой прямоугольной пластинке полупроводника с размерами порядка сантиметра. Под микроскопом такая пластинка СБИС похожа на план большого города. Интегральная схема имеет от нескольких десятков до нескольких сотен внешних контактов.
Для того, чтобы реализовать простые электронные часы, необходимо порядка 1000 вентилей, из 10000 вентилей уже можно собрать простейший центральный процессор, а современные мощные ЭВМ состоят из миллионов вентилей.
В качестве примера рассмотрим интегральную схему, которая реализует функцию сложение двух одноразрядных двоичных чисел. Входными данными этой схемы являются значения переменных x и y, а результатом – их сумма, которая, в общем случае, является двухразрядным числом (обозначим разряды этого числа как a и b), формирующиеся как результат сложения x+y. Запишем таблицу истинности для этой функции от двух переменных:
| x | y | b | a |
Легко вычислить, что величины a и b будут определяться формулами:
а = x<>y =(x or y) and not(x and y)
b = x and y
Реализуем нашу интегральную схему как набор вентилей, связанных проводниками (рис. 2.2. а).
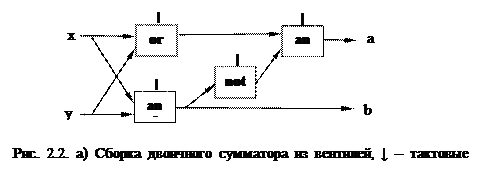 |
Наша интегральная схема (см. рис. 2.2 б) будет иметь не менее 7-ми внешних контактов: входные x и y, выходные а и b, один контакт для подачи тактовых импульсов, два контакта для подачи электрического питания (ясно, что без энергии ничего работать не будет) и, возможно, другие контакты. Суммирование чисел x и y в приведенной выше схеме осуществляется после прихода трёх тактовых импульсов (как говорят, за три такта). Современные компьютеры обычно реализуют более сложные схемы суммирования, срабатывающие за один такт.
Скорость работы интегральной схемы зависит от частоты прихода тактовых импульсов, называемой тактовой частотой. У современных ЭВМ тактовые импульсы приходят на схемы основной памяти с частотой примерно в сто миллионов раз в секунду, а на схемы центрального процессора – ещё примерно в 10 раз чаще.

3. Учебная машина
Рассмотрим конкретизацию абстрактной машины фон Неймана на примере учебной машины, которую будем называть УМ–3 (смысл этого названия – учебная машина трёхадресная). Наша учебная машина будет удовлетворять всем принципам фон Неймана.
Память учебной машины состоит из 512 ячеек, имеющих адреса от 0 до 511, по 32 двоичных разряда каждая. В каждой ячейке может быть записано целое или вещественное число (представляются они по-разному) или команда. Команда в ячейке будет представляться в следующей форме:
| КОП | A1 | A2 | A3 |
| 5 разрядов | 9 разрядов | 9 разрядов | 9 разрядов |
Здесь КОП – это число от 0 до 31, которое задаёт номер (код) операции, а A1, A2 и A3 – адреса операндов. Таким образом, в каждой команде задаются адреса аргументов (это A2 и A3)и адрес результата операции A1. Конкретизируем регистры устройства управления:
· RA – регистр, называемый счётчиком адреса, он имеет 9 разрядов и хранит адрес команды, которая будет выполняться вслед за текущей командой;
· RK – регистр команд имеет 32 разряда и содержит текущую выполняемую команду (код операции КОП и адреса операндов A1, A2 и A3);
· w – регистр «омега», в который после выполнения некоторых команд (у нас это будут арифметические команды сложения, вычитания, умножения и деления) записывается число от 0 до 2 по правилу (S – результат арифметической операции):
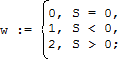
· Err – регистр ошибки, содержащий нуль в случае успешного выполнения очередной команды и единицу в противном случае.
В таблице 3.1 приведёны все команды учебной машины УМ–3.
Дата добавления: 2015-10-05; просмотров: 2249;
