Определение отношения теплоемкостей воздуха при постоянных давлении и объеме

I начало термодинамики утверждает, что количество теплоты, переданное термодинамической системе, идёт на увеличение её внутренней энергии и на работу, совершаемую силами, приложенными со стороны системы к внешним телам:

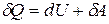. (4.1)

Элементарная работа, совершаемая газом при бесконечно малом изменении объёма 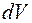, когда давление газа 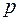можно считать неизменным, равна

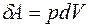. (4.2)

Для идеального газа элементарное изменение внутренней энергии 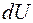определятся изменением его температуры 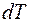и равно:

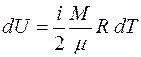, (4.3)
где 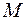– масса газа; 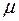– его молярная масса; 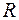– универсальная газовая постоянная, 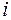– число степеней свободы молекул газа.

Числом степеней свободы 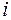называют число независимых координат, определяющих положение молекулы в пространстве. Например, число степеней свободы для одноатомной молекулы, равно трём, для жесткой двухатомной – пяти.

Количество теплоты 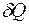, требуемое для нагревания газа, зависит от количества нагреваемого газа и от того, на сколько градусов должна быть изменена его температура. Поэтому для характеристики тепловых свойств газа используется теплоёмкость.

Удельной теплоёмкостью газа называется величина, равная количеств теплоты, которую необходимо сообщить единице массы газа для увеличения его температуры на 1 К:

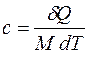. (4.4)

Теплоемкость одного моля вещества называется молярной теплоемкостью:

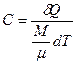. (4.5)

Значение теплоемкости газов зависит от условий их нагревания. Запишем I начало термодинамики и найдём теплоёмкости идеальных газов в различных термодинамических процессах.

В случае изохорного процесса 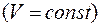I начало термодинамики принимает вид:

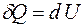. (4.6)
Учитывая (4.3) и (4.5), для молярной теплоёмкости при постоянном объёме получим:

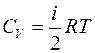. (4.7)

При изотермическом процессе ( 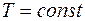), 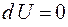и I начало термодинамики запишется так:

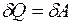. (4.8)
Теплоёмкость газа становится бесконечно большой 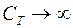. Это относится к идеальному изотермическому процессу, который возможен лишь при идеально хорошем обмене теплом между газом и внешними телами. Практически приблизиться к изотермическому процессу можно, заставляя его протекать настолько медленно, чтобы температура газа все время успевала выравниваться с температурой окружающих тел.

Если в газе протекает процесс изобарный ( 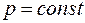), то I начало термодинамики имеет вид:

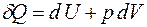(4.9)
или

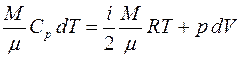. (4.10)

Из уравнения Менделеева- Клапейрона имеем

.
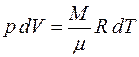Тогда из уравнения (4.10) для молярной теплоёмкости газа при постоянном давлении, получаем

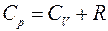. (4.11)

Таким образом, молярная теплоёмкость при постоянном давлении 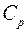превосходит молярную теплоёмкость при постоянном объёме 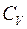на универсальную газовую постоянную 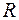. Это объясняется тем, что при нагревании газа при постоянном давлении газ расширяется. Сообщаемое ему извне тепло идёт не только на увеличение запаса его внутренней энергии 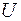, но и на совершение работы 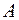против внешних сил.

Процесс, протекающий в газе без теплообмена с окружающей средой ( 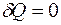), называется адиабатным. В этом случае I начало термодинамики имеет вид

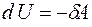
или

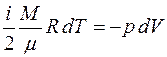. (4.12)
Из соотношения (4.12) следует, что при адиабатном сжатии газа ( 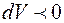), он нагревается ( 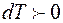); при адиабатном расширении ( 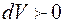) – газ охлаждается ( ).

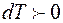Таким образом, при адиабатном изменении объёма газа его температура не остаётся постоянной, а молярная теплоёмкость газа
равна 0.

Cоответственный расчёт позволяет связать это изменение температуры 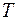с изменением его объёма 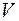. Пусть газ, занимая объём 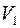, имел температуру 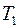, тогда при адиабатном изменении объёма до значения 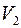, температура примет значение 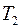, причём будет иметь место следующее соотношение:

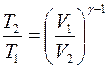, (4.13)

где 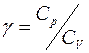, т. е. 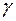есть отношение теплоёмкостей газа при постоянном давлении и постоянном объёме. Величина 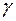называется показателем адиабаты.

Воспользовавшись формулой Менделеева-Клапейрона, справедливой для каждого данного состояния газа, получим:

;
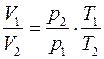подставив это значение 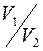в (4.13), получим:

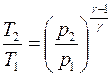. (4.14)

Формула (4.14), тождественная по своему смыслу с формулой (4.13), связывает изменение температуры, происходящее при адиабатном процессе, с изменением давления газа.

Приравнивая друг другу правые части выражений (4.13) и (4.14), получим

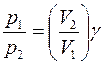или 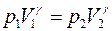, (4.15)
т.е. при адиабатном изменении объёма давление газа 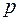меняется обратно пропорционально объёму, взятому в степени 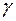. Формула (4.15) носит название формулы Пуассона.

Практически процессы не носят строго адиабатного характера, так как невозможно осуществить полной термической изоляции газа. Но поскольку для совершения теплообмена необходимо некоторое время, то адиабатным можно считать процесс, который протекает настолько быстро, что система не успевает вступить в теплообмен с окружающей средой.