Изучение дифракции когерентного излучения в параллельных лучах
Цель работы: изучение явления дифракции, определение диаметра отверстия, ширины щели, периода дифракционной решетки, определение длины волны лазерного излучения.
Оборудование:лазер, диафрагма, набор объектов для исследования (экран с круглым отверстием, экран со щелью, дифракционные решетки), поворотное зеркало, полупрозрачный экран.
Описание метода измерения
Дифракцией называется совокупность явлений, наблюдаемых при распространении света и в среде с резкими неоднородностями. Дифракция, в частности, приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. При прохождении света через преграды каждый элемент волнового фронта можно считать источником вторичных волн. Распределение интенсивности за преградой определяется интерференцией вторичных волн, проходящих в данную точку от всех элементов волновой поверхности, с учетом их амплитуды и фаз (принцип Гюйгенса-Френеля). Наблюдение дифракции осуществляется с помощью экрана, расположенного за преградой.
Различают дифракцию в параллельных лучах (дифракция Фраунгофера) и дифракцию в расходящихся лучах (дифракция Френеля). В этой работе рассматривается дифракция Фраунгофера.
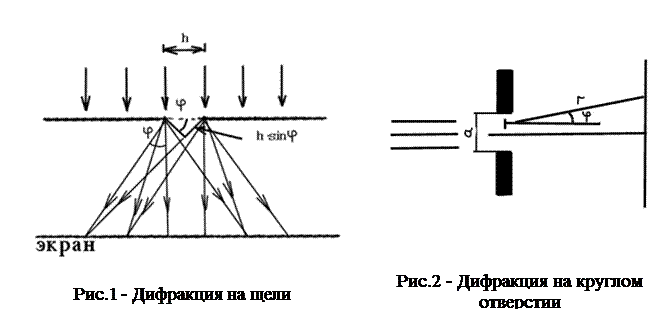
1. Дифракция на длинной узкой щели. Пусть параллельный монохроматический пучок света падает на щель шириной h (рис. 1). Тогда на экране за щелью будет наблюдаться дифракционная картина в виде чередующихся темных и светлых полос. С помощью построения, показанного на рис. 1, можно определить угол, под которым будет наблюдаться максимум интерференционной картины. В соответствии с принципом Гюйгенса Френеля можно рассматривать щель как систему вторичных источников (зон Френеля) S1. Если в направлении под углом 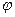 разность хода от соседних источников составляет
разность хода от соседних источников составляет 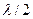 , то волны от этих источников, собранные линзой в одной точке экрана, гасят друг друга т.к. приходят в эту точку в противофазе. В случае четного числа источников, укладывающихся на ширине щели, в точке экрана, расположенной под углом
, то волны от этих источников, собранные линзой в одной точке экрана, гасят друг друга т.к. приходят в эту точку в противофазе. В случае четного числа источников, укладывающихся на ширине щели, в точке экрана, расположенной под углом 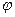 к первоначальному направлению распространения света будет наблюдаться минимум. Если же число источников нечетное, то остается один не скомпенсированный источник, и в этом случае под углом
к первоначальному направлению распространения света будет наблюдаться минимум. Если же число источников нечетное, то остается один не скомпенсированный источник, и в этом случае под углом 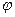 будет наблюдаться максимум. Оптическая разность хода лучей, идущих от крайних зон, равна
будет наблюдаться максимум. Оптическая разность хода лучей, идущих от крайних зон, равна  h sin
h sin 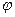 . Таким образом, условие минимума имеет вид
. Таким образом, условие минимума имеет вид
h sin 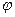 =
= 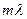 ,
,  (1)
(1)
условие максимума освещенности h sin 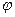 =
= 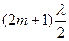 ,
, 
где 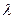 - длина волны света, m=0, ±1, ±2, ±3,… - порядки дифракционных минимумов. Очевидно, что по угловому расстоянию между дифракционными минимумами можно определить длину световой волны, если известна ширина щели, и наоборот.
- длина волны света, m=0, ±1, ±2, ±3,… - порядки дифракционных минимумов. Очевидно, что по угловому расстоянию между дифракционными минимумами можно определить длину световой волны, если известна ширина щели, и наоборот.
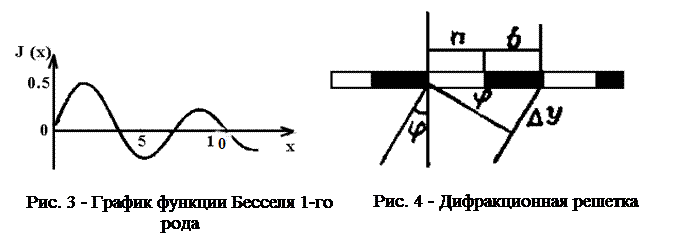
2. Дифракция на круглом отверстии. Согласно принципу Гюйгенса Френеля, для получения результирующей амплитуды под заданным углом 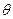 , необходимо просуммировать волны, излученные всеми участками этой круговой апертуры. Вклад каждого элемента отверстия в приближении Фраунгофера составляет cos(kr)*dA, где k=2
, необходимо просуммировать волны, излученные всеми участками этой круговой апертуры. Вклад каждого элемента отверстия в приближении Фраунгофера составляет cos(kr)*dA, где k=2 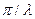 - волновое число, r – радиус-вектор (рис. 2), dA – элемент площади внутри апертуры. Амплитуда световой волны в точке, находящейся под углом
- волновое число, r – радиус-вектор (рис. 2), dA – элемент площади внутри апертуры. Амплитуда световой волны в точке, находящейся под углом 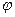 к первоначальному направлению распространения, определяется интегралом
к первоначальному направлению распространения, определяется интегралом
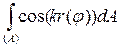 , (2)
, (2)
который не берется в элементарных функциях. Его решением является функция Бесселя первого рода J1(x). График этой функции представлен на рис. 3.
Первый минимум дифракционной картины соответствует условию J1(x)=0. В нашем случае x= 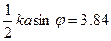 . Таким образом, условие первого минимума дифракции на круглом отверстии приобретает вид
. Таким образом, условие первого минимума дифракции на круглом отверстии приобретает вид
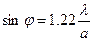 . (3)
. (3)
Аналогично можно получить условия минимумов и максимумов более высоких порядков. Положения нескольких первых максимумов и минимумов можно выразить приближенным условием
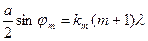 , (4)
, (4)
где m = 1,2,3,…, а – диаметр отверстия. Значения km для минимумов и максимумов приведены в таблице. Дифракционная картина представляет собой чередование светлых и темных колец. Сужение отверстия приводит к расплыванию дифракционной картины. При увеличении а дифракционная картина стягивается в точку.
| m | kmax | kmin |
| 0.61 | ||
| 0.41 | 0.56 | |
| 0.44 | 0.54 | |
| 0.46 | 0.53 |
3. Дифракционная решетка. Систему большого числа близких параллельных щелей называют дифракционной решеткой. Расстояние d=a+b (a – ширина щели, b – ширина промежутка между щелями) называется постоянной, или периодом, дифракционной решетки (рис. 4). Главные дифракционные максимумы возникают в тех направлениях, для которых оптическая разность хода лучей, идущих от соседних щелей решетки, равна целому числу длин волн 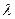
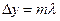 . (5)
. (5)
Из рис. 4 видно, что оптическая разность хода лучей Dy, идущих от двух соседних щелей под углом дифракции j, определяется выражением

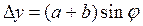 . (6)
. (6)
Таким образом, углы дифракции, под которыми наблюдаются максимумы, определяются условием
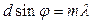 . (7)
. (7)
Здесь m = 0, ±1, ±2,… - порядок дифракционного максимума.
Описание установки
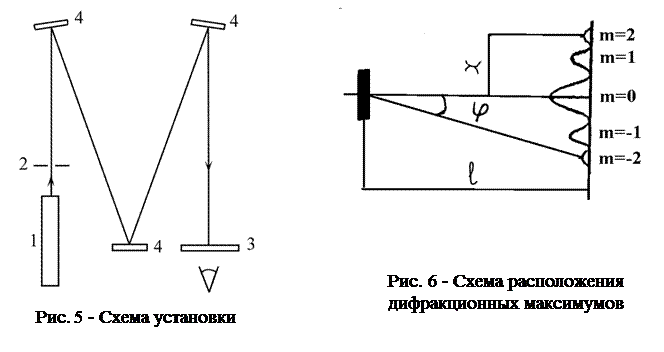
Оптическая схема установки представлена на рис. 5. Излучение лазера 1, проходит через диафрагму, роль которой играет колпачок – насадка на излучателе, и падает на объект 2 (щель, круглое отверстие или дифракционная решетка, которые в данной работе могут быть как вмонтированы в колпачок излучателя, так и предложены отдельно). Дифрагированный свет наблюдается на экране 3. Поскольку в работе используется когерентное излучение лазера, дифракционную картину можно наблюдать на экране без помощи линзы. Но в этом случае лучи, приходящие в одну точку экрана от разных зон, попадают туда под разными углами. Однако, если расположить экран на расстоянии много большем размеров области взаимодействия светового пучка с объектом
(удлинить путь луча позволяют поворотные зеркала 4), то можно считать, что все лучи приходят в заданную точку под одним и тем же углом j. Из рис. 6 видно, что
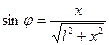 (8)
(8)
Измерив расстояние от объекта до экрана l и расстояние x от точки, соответствующей нулевому порядку дифракции (главному максимуму), до точки, соответствующей m-му порядку (рис. 6), можно определить размеры объектов по формулам (1), (4), (7), (8).
Итак, согласно вышесказанному, по расположению максисумов и длине волны можно определить размеры препятствий. А по отношению интенсивностей различных максимумов можно найти форму препятствий, например, форму штрихов решетки и различить пиловидную, прямолинейную и различные другие формы, даже не глядя на решетку. Этот принцип служит для определения положения атомов в кристалле, однако, из-за малых размеров препятствий необходимо применять излучение с очень малыми длинами волн, например, рентгеновские лучи.
Порядок выполнения работы
Упражнение 1. Изучение дифракции на щели.
1. Установить экран таким образом, чтобы лазерный пучок попадал на горизонтальную линию экрана.
2. С помощью поворотных зеркал получить на экране изображение дифракционных максимумов, расположить их симметрично относительно центра экрана.
3. Используя миллиметровую сетку, нанесенную на экране, измерить расстояние от середины нулевого максимума до минимума (рис. 6). Измерения провести для нескольких m. Результаты измерений занести в таблицу.
| m | ||||||
| xm, мм | ||||||
| l, мм | ||||||
| h, мм | ||||||
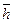 , мм , мм
|
4. По формулам (1) и (8) найти ширину щели h для каждого xm.
5. Вычислить среднее значение h.
6. Оценить погрешность измерений.
Упражнение 2. Изучение дифракции на круглом отверстии.
1. См. пункт 1 упражнения 1.
2. С помощью поворотных зеркал получить на экране изображение дифракционных колец, расположить их симметрично относительно центра экрана.
3. Измерить расстояние xm от нулевого до m-го максимума, используя миллиметровую сетку, нанесенную на экран. Измерения провести для нескольких m. Результаты измерений занести в таблицу.
| m | ||||||
| xm, мм | ||||||
| l, мм | ||||||
| a, мм | ||||||
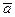 , мм , мм
|
4. По формулам (4) и (8) найти диаметр отверстия а для каждого xm.
5. Вычислить среднее значение диаметра отверстия 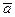 .
.
6. Оценить погрешность измерений.
Упражнение 3. Определение периода дифракционной решетки.
1. См. пункт 1 упражнения 1.
2. Получить на экране изображение дифракционных максимумов, (в случае использования дифракционных решеток с малым периодом, возможно, придется отказаться от системы зеркал и располагать экран непосредственно за решеткой).
3. Измерить расстояние xm от нулевого до m-го максимума, используя миллиметровую сетку, нанесенную на экран. Измерения провести для нескольких m. Результаты измерений занести в таблицу.
| m | ||||||
| xm, мм | ||||||
| l, мм | ||||||
| d, мм | ||||||
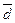 , мм , мм
|
4. По формулам (7) и (8) вычислить период дифракционной решетки d для каждого xm..
5. Вычислить среднее значение периода решетки 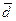 .
.
6. Оценить погрешность измерений.
Контрольные вопросы.
1. Что называется дифракцией света?
2. Основные виды дифракции. Какой из них изучается в данной работе?
3. Сформулируйте принцип Гюйгенса – Френеля.
4. Сформулируйте условие максимума для дифракции на длинной и узкой щели.
5. Как измерить диаметр отверстия с помощью явления дифракции?
6. Как влияет диаметр отверстия на размеры дифракционной картины?
7. Как измерить ширину щели с помощью явления дифракции?
8. Что такое дифракционная решетка?
9. Что называется периодом дифракционной решетки?
10. Сформулируйте условие максимумов для дифракционной решетки.
Дата добавления: 2015-09-29; просмотров: 1683;
