Клеедощатые арки
Арочные конструкции являются распространенными рациональными несущими конструкциями покрытий зданий пролетом 12-100 м. Арки относятся к распорным конструкциям, в которых распор воспринимается либо затяжкой, либо опорными нижележащеми конструкциями.
Основные геометрические схемы арок можно классифицировать по:
· статической схеме: трехшарнирные (статически определимые) и двухшарнирные (статически неопределимые);
· очертанию оси: круговые, стрельчатые, треугольные и др.;
· способу восприятия распора: непосредственно железобетонными фундаментам, несущим конструкциям каркаса здания; стальной затяжкой;
· типу поперечного сечения: сплошные (прямоугольные, двутавровые), спаренные, армированные и др.;
Основные схемы арок представлены на рис 6.1
Наиболее распространенные трехшарнирные арки, которые статически определимы и усилия в их сечениям не зависят от осадок опор, изменения температуры и деформаций затяжек.
Арки рассчитывают на сочетание постоянных снеговых и ветровых нагрузок.
Полное значение снеговой нагрузки на горизонтальную поверхность покрытия по СНиП «Нагрузки и воздействия» [2] по формуле
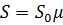 , (6.1)
, (6.1)
где 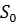 - расчетное давление снегового покрова на 1м2 горизонтальной поверхности земли; µ- коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие.
- расчетное давление снегового покрова на 1м2 горизонтальной поверхности земли; µ- коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие.
Схема распределения снеговой нагрузки и значения коэффициентов µ принимаются в соответствии с приложением 3 [2], при этом промежуточные значения коэффициентов µ определяются линейной интерполяцией. Снеговые нагрузки учитываются только на той части дуги арки, где угол наклона касательных к горизонту меньше 50°.
Для арок дугового очертания и близких к ним по форме схемы приложения нагрузок показаны на рис. 6.2.
Нормативное значение нормативной снеговой нагрузки определяется умножением расчетного значения на коэффициент 0,7.
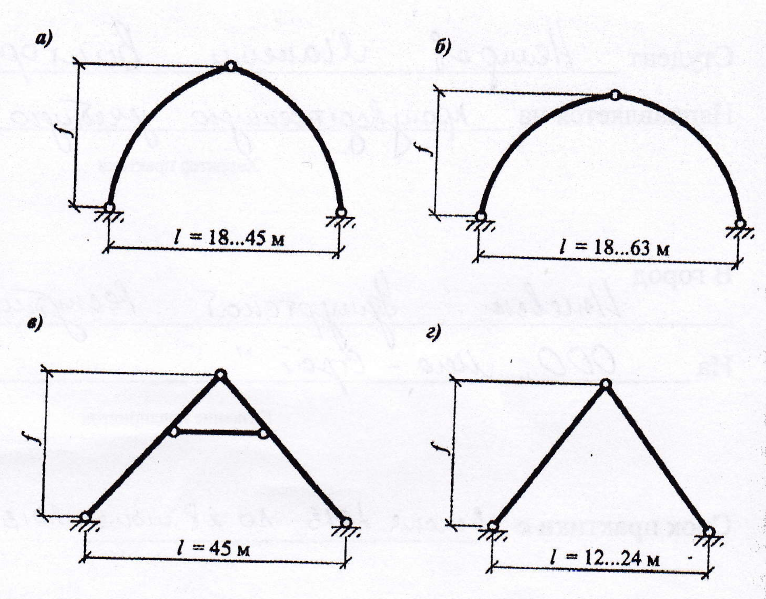
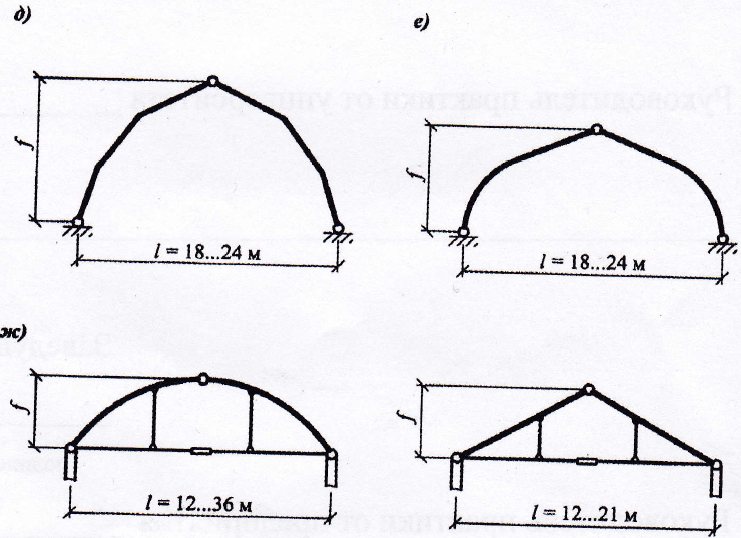
Рис. 6.1. Основные геометрические схемы арок: а) стрельчатые; б) круговые; в) распорная система треугольного очертания; г) треугольные; д) ломанные; е) параболические; ж) арки с затяжкой;
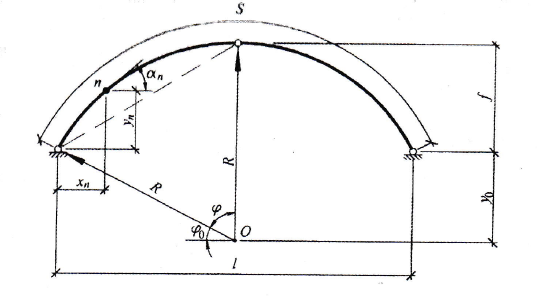
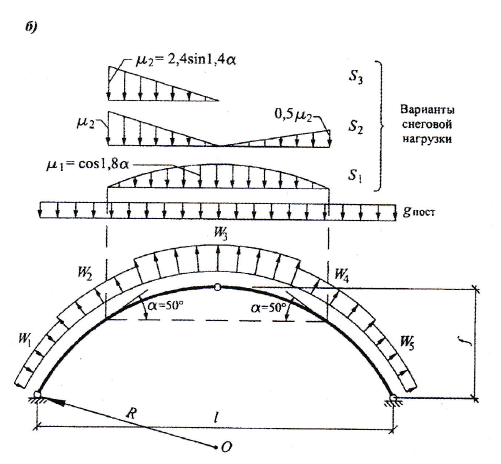
Рис. 6.2. Круговые арки: а) геометрическая схема;
б) схема приложения нагрузок
Расчетное значение ветровой нагрузки определяется согласно [2] определяется по формуле:
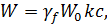 (6.2)
(6.2)
где 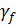 - коэффициент надежности по ветровой нагрузке;
- коэффициент надежности по ветровой нагрузке; 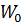 - нормативное значение ветрового давления;
- нормативное значение ветрового давления; 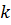 – коэффициент, учитывающий изменения ветрового давления по высоте;
– коэффициент, учитывающий изменения ветрового давления по высоте; 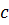 - аэродинамический коэффициент.
- аэродинамический коэффициент.
Криволинейные арки обычно делают с постоянным радиусом кривизны. Толщина досок арок принимается на более 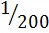 радиуса кривизны арки.
радиуса кривизны арки.
Радиус арки кругового очертания определяется по формуле
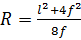 , (6.3)
, (6.3)
где 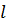 - пролет арки;
- пролет арки; 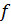 - стрела подъема арки.
- стрела подъема арки.
Для обеспечения поворота арок в узлах опорные и ключевые шарниры проектируются следующим образом:
1.Для арок пролетом до 30 м ключевой шарнир выполняется лобовым упором с использованием нагельного соединения (рис. 6.3). Для арок с затяжкой на опорах устанавливаются металлические башмаки (рис 6.4а). Для арок, определяющихся на фундаменты, опирания осуществляется непосредственным упором части торцевой поверхности арки (рис.6.4б).
2.При пролете арок более 30 м опорных и ключевых шарнирах устанавливаются металлические башмаки с плиточными или валиковыми шарнирами (рис. 6.5 и 6.6).
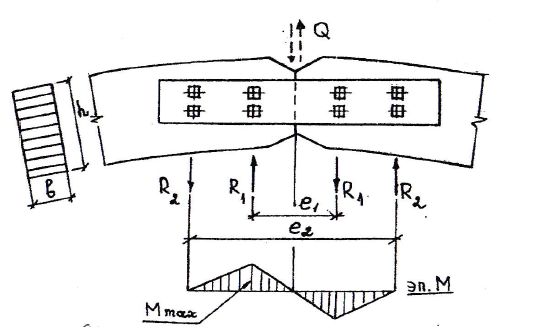
Рис. 6.3. Коньковый узел арки с деревянными накладками
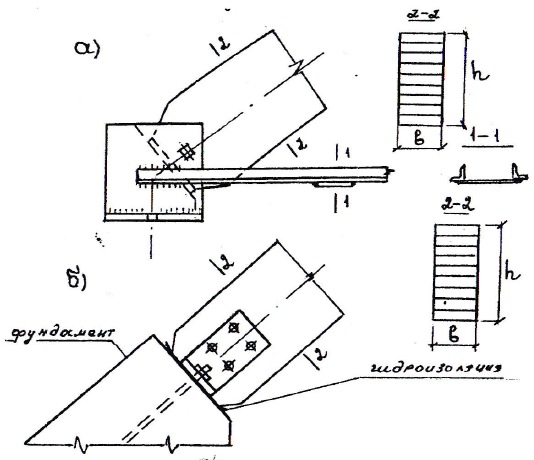
Рис. 6.4. Опорные узлы арки:
а) со стальным башмаком для арки с затяжкой; б) для арки без затяжки
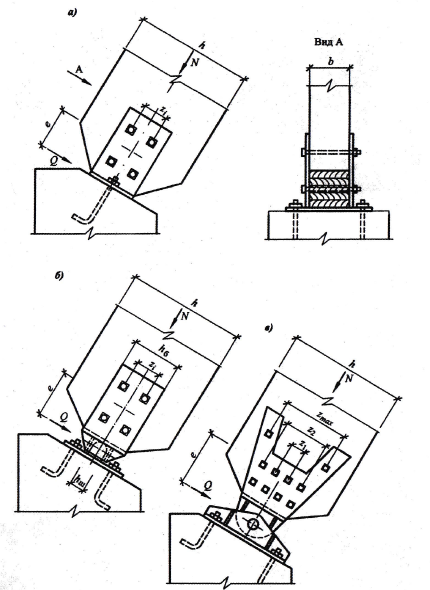
Рис. 6.5. Опорные узлы арок: а) простой лобовой упор; б) плиточный шарнир;
в) валиковый шарнир
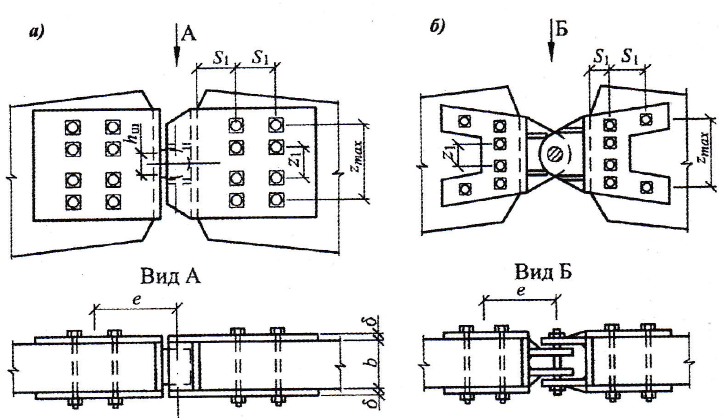
Рис. 6.6. Коньковые узлы арок, выполненные классическими шарнирами:
а) плиточный шарнир; б) валиковый шарнир (сварка стальных элементов условно не показана)
Статический расчет арок выполняется по общим правилам строительной механики. Значения внутренних усилий изгибающих моментов 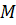 , поперечных
, поперечных 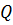 и нормальных
и нормальных 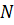 сил на расстоянии
сил на расстоянии 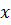 отоси опоры определяется (рис. 6.7) по формулам:
отоси опоры определяется (рис. 6.7) по формулам:
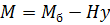 ;
; 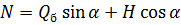 ;
; 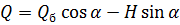 , (6.4)
, (6.4)
где 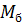 и
и 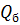 - изгибающий момент и поперечная сила в рассматриваемом сечении, определяемые как для балки с шарнирными закреплениям по концам и пролетом
- изгибающий момент и поперечная сила в рассматриваемом сечении, определяемые как для балки с шарнирными закреплениям по концам и пролетом 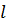 , равном пролету арки;
, равном пролету арки; 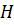 - распор арки.
- распор арки.
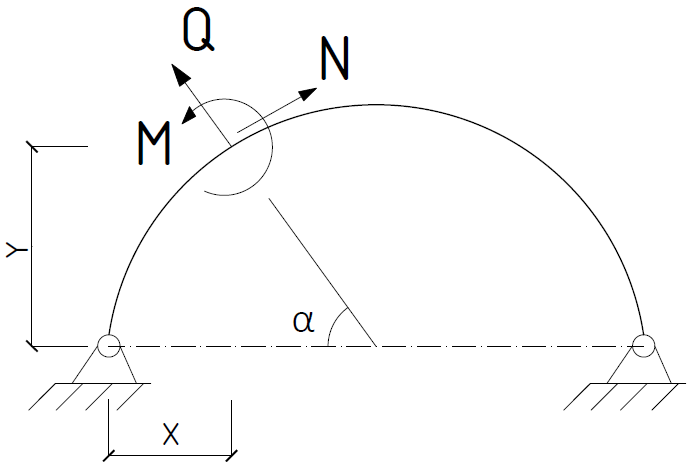
Рис.6.7. К статическому расчету арок
Подбор сечения арок производят по максимальному изгибающему моменту и продольной силе, действующей в том же сечении.
Расчет арки на несущую способность выполняется по методике сжато-изогнутого стержня (см. раздел 2.7).
Расчет на прочность сводится к выполнению условия
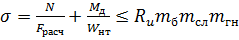 , (6.5)
, (6.5)
где 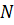 - расчетное значение продольной силы;
- расчетное значение продольной силы; 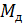 - изгибающий момент, определяемый из расчета по деформируемой схеме;
- изгибающий момент, определяемый из расчета по деформируемой схеме; 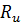 -расчетное сопротивление древесины изгибу;
-расчетное сопротивление древесины изгибу; 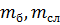 и
и 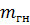 -соответственно коэффициенты, учитывающие высоту сечения, толщину слоя клееной древесины и кривизну арки;
-соответственно коэффициенты, учитывающие высоту сечения, толщину слоя клееной древесины и кривизну арки; 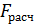 и
и 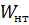 - расчетное значение площади сечения и момента сопротивления нетто.
- расчетное значение площади сечения и момента сопротивления нетто.
Расчетную длину арки в расчете на прочность по деформированной схеме принимают для 3-х шарнирной арки при симметричной нагрузке 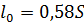 , где
, где 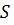 - длина дуги полуарки.
- длина дуги полуарки.
Расчет арки на устойчивость плоской формы деформирования выполняется по формуле (см. раздел 2.7).
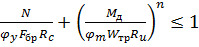 , (6.6)
, (6.6)
где 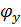 - коэффициент продольного изгиба полуарки из плоскости изгиба; расчетную длину сжатого элемента принимают равным
- коэффициент продольного изгиба полуарки из плоскости изгиба; расчетную длину сжатого элемента принимают равным 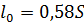 , где
, где 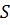 - длина дуги полуарки;
- длина дуги полуарки; 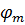 - коэффициент устойчивости элемента при изгибе.
- коэффициент устойчивости элемента при изгибе.
Клеевой шов проверяется на скалывание
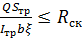 , (6.7)
, (6.7)
где 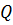 - расчетная поперечная сила;
- расчетная поперечная сила; 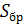 - статический момент полусечения относительно нейтральной оси;
- статический момент полусечения относительно нейтральной оси; 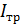 - момент инерции сечения брутто;
- момент инерции сечения брутто; 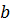 - ширина сечения;
- ширина сечения; 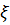 - коэффициент, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента (см. п.2.7).
- коэффициент, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента (см. п.2.7).
Коньковый узел рассчитывается на смятие от продольной силы 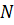 . Нагельное соединение в коньковом узле рассчитывается на поперечную силу
. Нагельное соединение в коньковом узле рассчитывается на поперечную силу 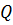 при несимметричном загружении арки.
при несимметричном загружении арки.
В случае решения узла с деревянными накладками (рис.6.3) поперечная сила воспринимается накладками, которые работают на поперечный изгиб. Величина максимального изгибающего момента равна
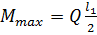 , (6.8)
, (6.8)
Усилия, действующие на болты, равны:
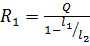 , (6.9)
, (6.9)
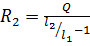 , (6.10)
, (6.10)
Требуемое число болтов в стыке по осям действия усилий 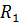 и
и 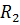 определяется по формуле:
определяется по формуле:
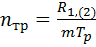 , (6.11)
, (6.11)
где 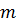 =2 число условных срезов одного болта;
=2 число условных срезов одного болта; 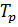 - расчетная несущая способность одного условного среза болта, определяемая согласно п.3.1.3.
- расчетная несущая способность одного условного среза болта, определяемая согласно п.3.1.3.
Дата добавления: 2015-09-25; просмотров: 4678;
