ИЗУЧЕНИЕ СПЕКТРА АТОМА ВОДОРОДА

Квантовомеханический подход к изучению процессов поглощения света атомами позволяет их исследовать и объяснить. Состояние атома в квантовой механике описывается волновой функцией φ_n, его энергия Е_n. В случае простейшего атома – атома водорода, состоящего из протона и электрона, квантовая механика позволяет получить точные решения волнового уравнения Шредингера (1).

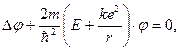
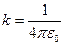, (1)

где m – масса электрона, е – его заряд, Е – полная энергия. Его решения для атома водорода дает набор дискретных уровней энергии. Для связанных состояний (Е_n<0):

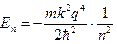, (2)

где 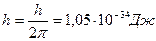, n =1,2,3,…- главное квантовое число.

С ростом n уровни энергии атома сближаются, в пределе при n дискретный спектр приближается к непрерывному, а квантовая система к классической. Это и есть принцип соответствия Бора, который позволяет выразить постоянную Ридберга через фундаментальные постоянные. Для простоты Бор принял, что в атоме водорода электроны вращаются вокруг протона по окружности радиусом r с циклической частотой ω:

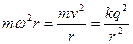, (3)

Согласно правилу квантования момента импульса электрона в атоме:

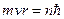(4)

Решение (3), (4) дает выражение для радиусов круговых орбит электронов в атоме водорода:

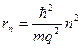, (5)

а также выражение (2).

Таким образом, при переходе атома водорода из состояния n₂ c энергией Е₂ в состояние n₁ с энергией Е₁ действует правило частот Бора:

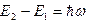, (6)

то есть испускается фотон с частотой ω и длиной волны λ:

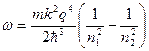, (7)

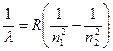, (8)

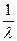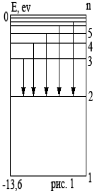
Формула (8) называется формулой Бальмера-Ритца. В этой формуле с увеличением n₂ разность между волновыми числами уменьшается, стремясь при n₂ к предельному значению (для n₁ = 2, 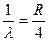). При этом линии сближаются, и уменьшается их интенсивность. Совокупность спектральных линий, закономерно меняющих свою интенсивность, называют спектральной серией. Предельное волновое число при n₂ называется границей серии. Визуально мы можем наблюдать только серию Бальмера: для водорода – n₁ = 2, n₂ = 3,4,5…(рис.1).