Системы растровой и векторной графики

Существуют два способа представления графического изображения:

- растровый (изображение со сложными гаммами цветов оттенков и форм: фотографии, рисунки, отсканированные данные);

- векторный (чертежи, изображения с простыми формами, тенями, окраской).

Изображения первого типа (растровые) представляют собой матрицу одинаковых по размеру прямоугольных элементов, каждый из которых обладает определенными цветовыми характеристиками. В результате получается своеобразная мозаика, выложенная из таких элементов — пикселей (Рисунок 10.3).

Рисунок 10.3. Растровое изображение и его фрагмент при большом увеличении

Растровое изображениепредставляет собой сетку, или растр, ячейки которой называются пикселями. Каждый пиксел в рас­тровом изображении имеет строго определенное положение и цвет (цветовое значение); любой объект интерпретируется про­граммой как набор окрашенных пикселов. При обработке рас­тровых изображений редактируются не конкретные объекты и контуры, а составляющие их группы пикселов.

Растровые изображения обеспечивают достаточно высокую точность передачи градаций цветов и полутонов, поэтому они являются оптимальным средством представления тоновых ори­гиналов, таких, как фотографии. Качество растровых изобра­жений напрямую зависит от разрешающей способности обору­дования — иными словами, для их представления всегда ис­пользуется фиксированное число пикселов. Это означает, что некорректная обработка такого изображения — например, произвольное изменение его размера или печать с более высо­ким разрешением — может привести к тому, что на оттиске мелкие детали будут потеряны, а границы объектов получатся неровными.

Разрешающая способность – это количество элементов в заданной области.

Имеются:

- разрешающая способность графического изображения;

- разрешающая способность принтера как устройства вывода;

- разрешающая способность мыши как устройства ввода.

Растр или растровый массив (bitop) представляет совокупность битов, расположенных на сетчатом поле-канве. Бит может быть включен (единичное состояние) или выключен (нулевое состояние).

Состояние битов можно использовать для представления черного или белого цветов, так, что, соединив на канве несколько битов, можно создать изображение из черных и белых точек. Растровое изображение напоминает лист клетчатой бумаги, на котором каждая клеточка закрашена черным или белым цветом, в совокупности формируя рисунок. Основным элементом растрового изображения является пиксель (pixel). Под этим термином часто понимают несколько различных понятий: отдельный элемент растрового изображения, отдельная точка на экране монитора, отдельная точка на изображении, напечатанном принтером.

Цвет каждого пикселя растрового изображения – черный, белый, серый или любой из спектра – запоминается с помощью комбинации битов. Размер изображения описывает физическую длину и ширину изображения, которая измеряется в пикселах.

Разрешение – это плотность размещения пикселов, которая измеряется в точках на дюйм (dpi). Эта величина представляет собой расстояние между соседними пикселами. Чем больше битов используется для этого, тем большее количество оттенков цветов для каждого пиксела можно получить. Число битов используемых компьютером для хранении информации о каждом пикселе, называется битовой глубиной или глубиной цвета.

Наиболее простой тип растрового изображения состоит из пикселов, имеющих два цвета – черный и белый. Для хранения такого типа пикселов требуется 1 бит в памяти компьютера, поэтому изображение, состоящее из пикселов такого вида, называется однобитовым изображением. Для отображения большого количества цветов используются больше битов информации.

Основной недостаток растровой графики состоит в том, что каждое изображение для своего хранения требует большое количество памяти. Другой недостаток – снижение качества изображения при масштабировании.

Масштабирование изображения заключается в изменении вертикального и горизонтального размеров изображения. Масштабирование может быть пропорциональным – в этом случае соотношение между высотой и шириной рисунка не изменяется, а меняется общий размер, и непропорциональным – в этом случае оба измерения измеряются по-разному.

Масштабирование растровых рисунков является намного более сложным процессом, чем для векторной графики, и часто сопровождается потерей качества. При изменении размеров растрового изображения выполняется одно из следующих действий:

- одновременное изменение размеров всех пикселов (в большую или меньшую сторону);

- добавление или убавление пикселов из рисунка для отражения производимых в нем изменений, называемое выборкой пикселов в изображении.

Простейший способ изменения масштаба растрового рисунка состоит в изменении размера всех его пикселов.

При масштабировании изображения количество входящих в него пикселов не меняется, а изменяется количество создаваемых устройством вывода элементов, идущих на построение отдельного пиксела изображения.

Выборка растрового рисунка может быть сделана двумя различными способами:

- по первому – дублируется или удаляется необходимое количество пикселов. При этом в результате масштабирования ухудшается качество изображения.

- по второму – с помощью определенных вычислений можно создать пикселы другого цвета, определяемого цветами первоначального пиксела и его окружения. Этот метод называется интерполяцией и является более сложным, чем простое дублирование. При интерполяции кроме дублируемых пикселов отбираются и соседние с ними, с помощью которых вновь создаваемые пикселы получают от существующих усредненный цвет или оттенок серого.

Растровый способ лучше всего подходит для изображений с большим количеством деталей и сложными цветовыми переходами, в частности для фотографий. В современной компьютерной графике он является самым распространенным. Однако существуют области, где предпочтительнее использовать векторную графику.

Векторное представление изображения кардинально отличается от растрового. Его принцип состоит в том, что описываются только основные точки изображения, а промежуточные достраиваются между ними по определенным математическим законам. Например, если необходимо нарисовать прямую, то можно указать только координаты концов отрезка, а также сделать пометку, что соединяющая их линия — прямая. Для описания окружности достаточно задать ее центр, указать радиус и сделать пометку «окружность». Аналогичным образом кодируются цвет объекта, толщина линий и пр. В таком виде информация хранится в файле, а когда приходит время отобразить графический элемент на мониторе, на бумаге или ином носителе, выводное устройство строит недостающие элементы изображения в соответствии с инструкциями.

Для описания векторного графического объекта существует множество способов. Самый удобный и распространенный из них — так называемые кривые Безье. Придумал эту модель в 1968 году французский инженер-математик Пьер Безье для решения узкоспециальной задачи — простого описания сложных двумерных фигур для машин по обработке листового металла. Способ оказался настолько удачным, что завоевал популярность далеко за пределами инженерной графики. Его суть сводится к следующему. Любая геометрическая фигура (традиционно она называется Path (Путь)) разбивается на несколько относительно простых участков (сегментов). Каждый сегмент начинается и заканчивается особой (якорной) точкой. В файле явно описываются координаты якорных точек, а также первая и вторая производные выходящего из них сегмента. На рисунке 10.4 изображен фрагмент кривой Безье.

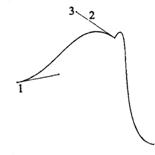
Рисунок 10.4. Фрагмент кривой Безье

Якорные точки — это маленькие белые квадраты (1), из которых выходят вспомогательные прямые (2). Эти отрезки называют Control Handle (Направляющая линия). Каждая направляющая заканчивается черной точкой — маркером (3), ее длина и направление как раз и соответствуют первой и второй производным. Для того, чтобы изменить форму сегмента, достаточно потянуть за маркер соответствующей направляющей.

Векторное представление определяет описание изображения в виде линий и фигур, возможно, с закрашенными областями, заполняемыми сплошным или градиентным цветом. В векторной графики для описания объектов используются комбинации компьютерных команд и математических формул для описания объектов.

Векторную графику называется объектно-ориентированной или чертежной графикой. Достоинствами векторной графики являются:

- описание объекта является простым и занимает мало памяти;

- простота масштабирования изображения без ухудшения его качества;

- независимость объема памяти требуемой для хранения изображения от выбранной цветовой модели.

Недостатком – некоторая искусственность, заключающая в том, что любое изображение необходимо разбить на конечное множество составляющих его примитивов.

Масштабирование векторных рисунков выполняется просто и без потери качества. Так как объекты векторной графики создаются по их описаниям, то для изменения масштаба векторного объекта достаточно изменить его описание. Например, чтобы увеличить в 2 раза векторный объект, следует удвоить значение, описывающее его размер.

Векторные изображения не зависят от разрешения — иными словами, они не определяются с помощью фиксированного ко­личества пикселов и на любом оборудовании всегда воспроизво­дятся с максимально возможным качеством. Векторные програм­мы являются наилучшим средством для создания шрифтовых (особенно с использованием мелких кеглей) и высокоточных графических объектов, например, логотипов, для которых прин­ципиально важное значение имеет сохранение четких, ясных контуров независимо от размера изображения.

Заметим, что экран компьютера представляет собой растро­вую сетку, поэтому как битовые, так и векторные изображения воспроизводятся на нем с помощью пикселов. Для отображения на экране векторные программы представляют все объекты в виде наборов пикселов.

У каждого способа представления графического изображения, как уже отмечалось выше, есть свои преимущества. Растровый позволяет передавать тонкие, едва уловимые детали образов, векторный же лучше применять, если оригинал имеет отчетливые геометрические очертания. Векторная графика все больше используется для Интернета, так как при соблюдении определенных условий размер ее файлов очень незначителен, что крайне важно при передаче информации по сетям. Но растровые файлы быстрее вырисовываются на экране дисплея, так как для вывода векторного изображения процессору необходимо произвести множество математических операций. С другой стороны, векторные файлы гораздо проще редактировать.

Среди современных программных продуктов, традиционно относящихся к сфере векторной графики, на самом деле трудно встретить «чисто» векторные редакторы: все приложения в большей или меньшей мере могут работать с растровыми объектами, текстом и другими элементами.

Векторная и растровая графика существуют не обособленно друг от друга. Векторные рисунки могут включать в себя и растровые изображения, могут быть преобразованы друг в друга. В этом случае говорят о конвертации графических файлов в другие форматы. Не всегда осуществимо преобразование растровой графики в векторную.

Различают три вида компьютерной графики: растровую графику, векторную графику и фрактальную графику. Они отличаются принципами формирования изображения при отображении на экране монитора или при печати на бумаге.

Растровую графику применяют при разработке электронных (мультимедийных) и полиграфических изданий. Иллюстрации, выполненные средствами растровой графики, редко создают вручную с помощью компьютерных программ. Чаще для этой цели используют сканированные иллюстрации, подготовленные художником на бумаге, или фотографии. В последнее время для ввода растровых изображений в компьютер нашли широкое применение цифровые фото- и видеокамеры. Большинство графических редакторов, предназначенных для работы с растровыми иллюстрациями, в большей мере ориентированы не на создание изображений, сколько на их обработку. В сети Интернет применяются только растровые иллюстрации.

Программные средства для работы с векторной графикой предназначены, в первую очередь, для создания иллюстраций и в меньшей степени для их обработки. Такие средства широко используют в рекламных агентствах, дизайнерских бюро, редакциях и издательствах. Оформительские работы, основанные на применении шрифтов и простейших геометрических элементов, решаются средствами векторной графики намного проще. Существуют примеры высокохудожественных произведений, созданных средствами векторной графики, но они скорее исключение, чем правило, поскольку художественная подготовка иллюстраций средствами векторной графики чрезвычайно сложна.

Программные средства для работы с фрактальной графикой предназначены для автоматической генерации изображений путем математических расчетов. Создание художественной фрактальной композиции состоит не в рисовании или оформлении, а в программировании. Фрактальную графику редко применяют для создания печатных или электронных документов, но ее часто используют в развлекательных программах.

Простейшим фрактальным объектом является фрактальный треугольник. Попробуем построить обычный равносторонний треугольник со стороной а. Разделим каждую из его сторон на три отрезка. На среднем отрезке стороны построим равносторонний треугольник со стороной, равной 1/3 стороны исходного треугольника, а на других отрезках построим равносторонние треугольники со стороной, равной (1/9)*a. С полученными треугольниками повторим те же операции. Можно заметить, что треугольники последующих поколений наследуют свойства своих родительских структур. Так рождается фрактальная фигура.

Процесс наследования можно продолжать до бесконечности. Взяв такой бесконечный фрактальный объект и рассмотрев его в лупу или микроскоп, можно найти в нем все новые и новые детали, повторяющие свойства исходной структуры.

Фрактальными свойствами обладают многие объекты живой и неживой природы. Обычная снежинка, многократно увеличенная, оказывается фрактальным объектом. Фрактальные алгоритмы лежат в основе роста кристаллов и растений. Взгляните на ветку папоротникового растения, и вы увидите, что каждая дочерняя ветка во многом повторяет свойства ветки более высокого уровня.

В отдельных ветках деревьев чисто математическими методами можно проследить свойства всего дерева. А если ветку поставить в воду, то вскоре можно получить саженец, который со временем разовьется в полноценное дерево (это легко удается сделать с веткой тополя).

Способность фрактальной графики моделировать образы живой природы вычислительным путем часто используют для автоматической генерации необычных иллюстраций.