Квантование по уровню. При квантовании по уровню непрерывное множество значений функции x(t) заменяется множеством дискретных значений

При квантовании по уровню непрерывное множество значений функции x(t) заменяется множеством дискретных значений. Для этого в диапазоне непрерывных значений функции x(t) выбирается конечное число дискретных значений этой функции (дискретных уровней) и в процессе квантования значение функции x(t) в каждый момент времени заменяется ближайшим дискретным значением. В результате квантования образуется ступенчатая функция x_g(t).

Квантование по уровню практически может осуществляться двумя способами. При первом способе квантования мгновенное значение функции x(t) заменяется меньшим дискретным значением. При втором способе квантования мгновенное значение функции x(t) заменяется ближайшим меньшим или большим дискретным значением в зависимости от того, какое из этих значений ближе к мгновенному значению функции. В этом случае переход ступенчатой функции с одной ступени на другую происходит в те моменты, когда первоначальная непрерывная функция x(t) пересекает середину между соответствующими соседними дискретными уровнями.

Расстояние между дискретными соседними уровнями называется интервалом или шагом квантования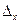

Различают равномерное квантование по уровню, при котором шаг квантования постоянен, и неравномерное квантование по уровню, когда шаг квантования непостоянен. На практике преимущественное применение получило равномерное квантование в связи с простотой его технической реализации.