Електричний дипольта його поле

Якщо система з двох різнойменних точкових зарядів величиною q, відстань між якими l, розглядається на відстані r>>l, то вона називається диполем. Величина l ¾ плече диполя. Диполь характеризується вектором дипольного моменту 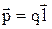, направленим від від'ємного заряду до додатного.

Важливість розгляду електричного поля диполя зумовлюється тим, що природні джерела електромагнітного випромінювання можна моделювати електричним диполем. Така модель може достатньо точно описати енергію джерел як функцію просторових координат та часу.

9.8.1. Потенціал електричного поля диполя

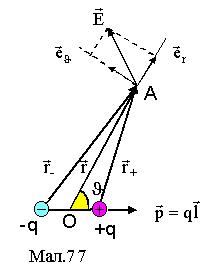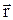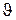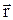Знайдемо потенціал та напруженість електричного поля диполя в точці А з радіус-вектором відносно середини плеча диполя О та кутом між та моментом 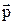(див. Мал.77). Потенціал системи двох точкових зарядів у точці А дорівнює алгебраїчній сумі потенціалів, створених кожним із зарядів

,

,

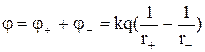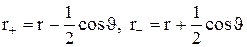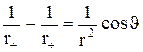
Ми поклали, що 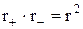, бо r >> l. Тепер

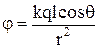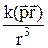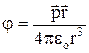= , або , (1)

9.8.2. Напруженість електричного поля диполя

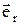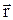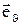
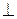
Напруженість поля визначимо через потенціал (1) за формулою . Можна ввести таку систему координат, в якій указана формула є достатньо простою. Такою системою координат є система базисних ортонормованих векторів || та 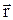. Вектор 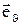направлений у сторону зростання кута 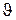. Оператор 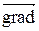у цих координатах має складовими

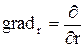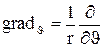, . (2)

Відповідні компоненти напруженості (2) запишуться у вигляді

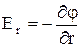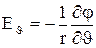, . (3)

Продиференціювавши j із (1) по відповідним змінним, одержимо

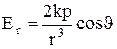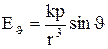, . (4)

Величину напруженості Е знайдемо з виразу

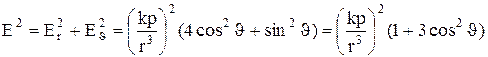
або

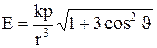. (5)

Напруженість у точках на прямій, на якій лежить диполь ( 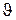= 0 або 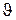= p) дорівнює

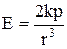, (6)

а в точці, що знаходиться на осі диполя ( )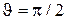

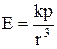. (7)

9.8.3. Диполь у неоднорідному електричному полі

На заряди диполя, розміщеного в електростатичному полі з напруженістю 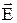(див.Мал.78) діє пара сил величиною 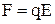й плечем 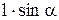, які створюють момент сили величиною

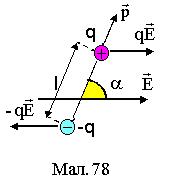
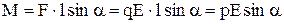, (8)

що діє на диполь (див.Мал.13). Вектор моменту сили, з огляду на (8), запишеться так

.

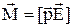При повороті диполя на кут 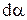, поле виконує роботу

.

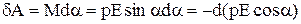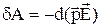(9)

Ця робота виконується зовнішнім полем на створення механічної потенціальної енергії W_м диполяв електричному полі

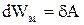. (10)

Підставляючи (8) у (9), одержимо

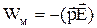(11)

Якщо зовнішнє поле з напруженістю 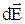створює дипольний момент 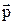, поляризуючи неполярні молекули або, розвертаючи дипольний момент полярних молекул, то при цьому виконується робота

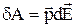. (12)

В неоднорідному полі, коли 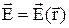, на диполь діє сила

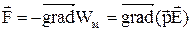, (13)

яка втягує його в область більшої величини напруженості. Зокрема, коли 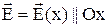, маємо

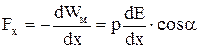. (14)

9.9. Потік вектора напруженості, теорема Остроградського-Гауса

9.9.1. Просторовий (тілесний) кут

Розглянемо сферу й конус, вершина якого співпадає з центром сфери О, а твірна конуса більше радіуса сфери (див.Мал.79). Під тілесним (просторовим) кутом 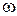розуміють частину простору, обмежену бічною 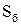поверхнею конуса. Мірою тілесного кута 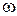є відношення поверхні сфери 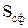, вирізаної ним до 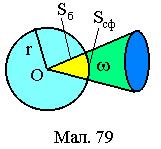квадрата радіуса r

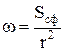. (1)

Тілесний кут має одиницею вимірювання — стерадіан (стрд). Якщо вирізана конусом поверхня сфери 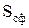дорівнює 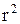, то тілесний кут дорівнює 1 стрд. Просторовий кут, що спирається на всю поверхню сфери 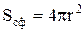дорівнює 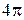стрд.

9.9.2. Потік вектора напруженості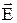

Нехай в електростатичному полі є елементарна поверхня 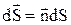з нормаллю 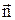, яку пронизує силова лінія напруженості 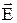(див.Мал.80). Елементарний потік Ф вектора напруженості 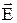через цю поверхню визначається так

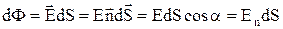, (2)

де 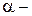кут між 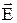та нормаллю 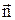до dS , .

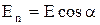Якщо напруженість 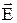створена точковим зарядом dq, то її величина дорівнює 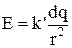і (2) можна записати у вигляді

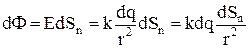, (3)

В (3) 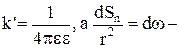тілесний кут, що спирається на поверхню dS і з урахуванням цього (3) запишеться так

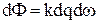. (4)

Потік вектора напруженості Е, створеного точковим зарядом dq для довільної поверхні S записується у вигляді

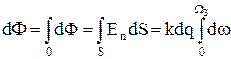, (5)

де 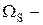тілесний кут, що спирається на поверхню S.