Исследование спектра излучения атома водорода

Первые исследования спектров атома водорода были выполнены И. Бальмером в 1885 г., которые показали, что спектр атомов водорода является линейчатым, а известные в то время девять линий в видимой части спектра удовлетворяют формуле:

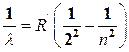, (1)

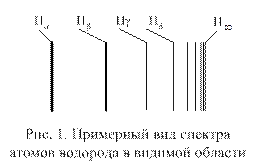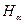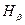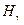
где R′ = 10973731,77 м^-1; n = 3,4, … . Константа R′ была определена экспериментально Й. Ридбергом и называется постоянной Ридберга. На рис. 1 приведен примерный вид спектра атомов водорода в видимой области спектра, где символами , , 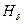обозначены первые четыре линии этого спектра. Символом 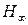обозначена линия с минимальной длиной волны в этой области спектра.

Дальнейшие исследования спектров атомов водорода обнаружили излучение водорода в ультрафиолетовой (Лайман) и инфракрасной (Пашен, Брэкет, Пфунд, Хэмфри) областях спектра. Причем все эти линии располагаются сериями и могут быть описаны формулой

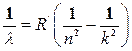, (2)

где n и k – целые числа. Эта формула называется формулой Бальмера–Ридберга. Для серии Лаймана n = 1, для серии Бальмера n = 2, для серии Пашена n = 3 и т.д.

Законы классической электродинамики не позволяют объяснить дискретный характер спектров излучения атомов.

Вращающийся по орбите электрон согласно классической электродинамике непрерывно излучает электромагнитные волны. При этом энергия его должна непрерывно уменьшаться, непрерывно также изменяется и частота обращения электрона вокруг ядра, следовательно, спектр излучения атома должен быть непрерывным. Истратив энергию на излучение, электрон должен упасть на ядро и атом как физический объект исчезает. В действительности же атом является устойчивой системой. Кроме того, из эксперимента следует, что спектр излучения атома водорода является линейчатым.

Преодоление этих трудностей было впервые разрешено теорий Н. Бора. Отметим сразу, что полное непротиворечивое объяснение спектральных закономерностей, как в спектре атомного водорода, так и других химических элементов было дано лишь квантовой механикой. Но поскольку в объяснении спектральных закономерностей в атоме водорода эти теории дают одинаковый результат, то здесь мы ограничимся кратким рассмотрением теории атома водорода по Н. Бору.

Основу теории Бора составили три постулата и классическая механика Ньютона. На основании того, что атомные спектры представляют собой набор отдельных линий, соответствующих дискретному набору частот 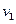, , 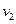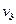...., Бор сделал вывод, что атомы не могут обладать энергией, способной изменяться непрерывно, и сформулировал следующие постулаты:

1. Постулат стационарных состояний. В атоме существуют стационарные (не изменяющиеся со временем) состояния, характеризующиеся определенными дискретными значениями энергии, в которых он не излучает и не поглощает энергию.

2. Постулат квантования орбит. В стационарных состояниях атома электрон может двигаться лишь по таким орбитам, для которых момент импульса электрона имеет дискретные значения, удовлетворяющие условию:

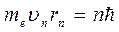, (3)

где n = 1,2,3 … , 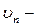скорость электрона по n-ой орбите радиуса 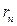, 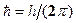– постоянная Планка.

3. Постулат частот. При переходе электрона из одного стационарного состояния в другое стационарное состояние излучается (поглощается) один фотон с энергией, равной разности энергий соответствующих стационарных состояний 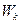и :

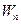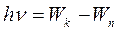. (4)

При 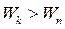происходит излучение энергии, при 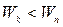- поглощение энергии. Набор возможных квантовых переходов и определяет линейчатый спектр атома:

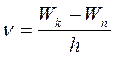(5)

Используя постулаты Бора и второй закон Ньютона, можно получить выражение для полной энергии электрона в атоме водорода, а также водородоподобного атома[1] в виде, см. подробнее, например [1,2]:

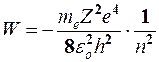(6)

Из формулы (6) следует, что полная энергия электрона в атоме водорода отрицательна и образует дискретную, прерывистую последовательность значений, изменяющихся в зависимости от числа n. Целое число n в выражении (6), определяющее энергетические уровни атома, называется главным квантовым числом. Энергетическое состояние с n = 1 является основным, или нормальным, состоянием; состояния с n > 1 являются возбуждёнными.

Придавая n различные целочисленные значения, получим для атома водовода согласно формуле (6) возможные уровни энергии, схематически представленные на рис. 2.

Так как полная энергия электрона в атоме водорода отрицательна, то с увеличением n уменьшение её абсолютного значения соответствует возрастанию энергии. С ростом n энергетические уровни электрона сближаются к границе, соответствующей значению n = ∞.

Атом водорода обладает, таким образом, минимальной энергией при n = 1 (W₁ = -13,55 эВ) и максимальной при n = ∞ (W_∞ = 0), т.е. при удалении электрона из атома. Следовательно, значение W_∞ = 0 соответствует ионизации атома (отрыву от него электрона). Разность между энергией ионизированного атома и энергией основного состояния называется энергией ионизации:

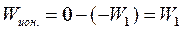. (7)

Согласно постулату частот Бора (4) при переходе атома водорода из стационарного состояния k с большей энергией в стационарное состояние n с меньшей энергией испускается квант с частотой:

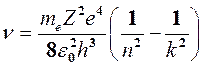. (8)

Подставляя в формулу (2) или (8) n = 1 и k = 2,3,4…, получим группу спектральных линий, образующих серию Лаймана и соответствующих переходам электронов с возбуждённых уровней (k = 2, 3, 4…) на основной уровень (n = 1). Аналогично, при подстановке n = 2, 3, 4, 5, 6 получим серии Бальмера, Пашена, Брэкета, Пфунда и Хэмфри (часть из них схематически представлена на рис. 2). Серия Лаймана (n = 1) лежит в ультрафиолетовой области спектра, серия Бальмера (n = 2) в видимой области спектра, все другие (n = 3, 4, 5, 6) в инфракрасной области.

Выражая частоту спектральной линии ν через длину волны λ, 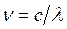, формулу (8) можно представить в виде:

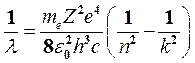. (9)

Сравнивая теоретическое (9) и экспериментальное (2) выражения, видим, что они совпадают, если положить стоящую перед скобкой комбинацию констант в формуле (9) равной постоянной Ридберга R^′:

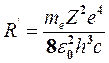. (10)

Из формулы (10) следует, что константа R^′ выражается в обратных метрах. В учебной и научной литературе наряду с постоянной Ридберга R^′ используют постоянную Ридберга R, выражаемую в обратных метрах, они связаны соотношением:

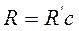, (11)

где с – скорость света в вакууме, с = 299792458 м/с. Отметим, что в данной работе удобнее экспериментально определять постоянную Ридберга R′ на основе измерений длины волны.