Додавання двох коливань одного напрямку
Для додавання двох коливань одного напрямку, наприклад, вздовж осі ОХ
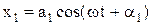 , (1)
, (1)
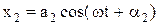 , (2)
, (2)
застосуємо метод векторної діаграми. Математично це виражається в знаходженні величини суми двох векторів, довжини яких чисельно рівні амплітудам коливань, із подальшим знаходженням проекції х результуючого вектора (див.Мал.28). Цю процедуру проведемо в такому вигляді
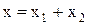 , (3)
, (3)
причому
 , (4)
, (4)
де
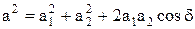 , (5)
, (5)
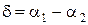 . (6)
. (6)
Початкову фазу a можна визначити з виразу
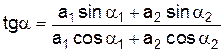 . (7)
. (7)
Одержаний результат випливає з наступних міркувань. Рівняння для х1 та х2 можна записати у експоненціальному комплексному вигляді:
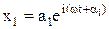 ,
, 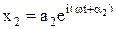 ,
,
і тоді

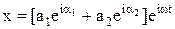 . (8)
. (8)
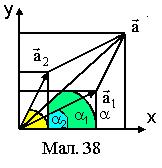 З (8) видно, що знаходження х зводиться до знаходження модуля а та аргумента a комплексного числа
З (8) видно, що знаходження х зводиться до знаходження модуля а та аргумента a комплексного числа
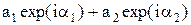 . (9)
. (9)
Це легко зробити, пригадавши, що сума двох комплексних чиселзнаходиться в комплексній площині, як сума двох векторів, що визначають ці числа (див.Мал.38). Звідси амплітуда
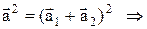
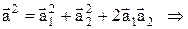
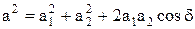 ,
,
де 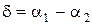 ¾ кут між векторами
¾ кут між векторами 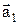 та
та 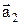 . Проекція
. Проекція 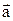 на вісь ОХ:
на вісь ОХ:
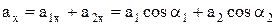 ,
,
а на вісь ОУ:

і
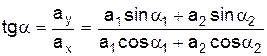 .
.
Два коливання з частотами w1=w2=w називаються когерентними, якщо різниця їх фаз є сталою величиною, тобто
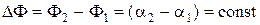 ,
,
або такою що за період T вона змінюється на величину меншу 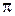 . При цьому буде відмінним від 0 інтерференційний доданок
. При цьому буде відмінним від 0 інтерференційний доданок 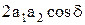 в (5).
в (5).
При додаванні двох когерентних гармонічних коливань результуюче коливання буде гармонічним із тією ж частотою w.
В залежності від значення різниці початкових фаз d, амплітуда результуючого коливання може змінюватися в межах від
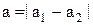 ,
,
коли  , до величини
, до величини
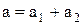 ,
,
коли 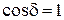 ,
, 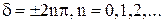 .
.
У першому випадку коливання відбуваються у проти фазі і їх сума має мінімальну амплітуду, а у другому випадку коливання відбуваються у фазі, і їх сума має максимальну амплітуду.
При додаванні N гармонічних коливань одного напрямку з кратними частотами wn=nw, n=1,2,3,... одержимо періодичні, гармонічні коливання з періодом Т=2p/w. І, навпаки, кожне періодичне коливання з періодом Т можна представити як суму нескінченного числа простих гармонічних коливань із частотами, кратними основній частоті 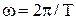 .
.
Коливання з частотами, більшими w, називаються гармоніками. Сукупність таких гармонік утворює спектр коливань, який має дискретний характер. В той же час, неперіодичне коливання також можна представити у вигляді розкладу по гармонічним коливанням, в яких спектр частот буде неперервним (суцільним) із частотами в деякому інтервалі (w1,w2).
4.9. Додавання двох взаємно перпендикулярних коливань
Додавання двох взаємно перпендикулярнихза напрямком коливань матеріальної точки математично зводиться до знаходження траєкторії руху точки на площині F(x,y)=0, методом виключення часу t, як параметру. Наприклад, розглянемо коливання матеріальної точки, яке задається на площині рівняннями
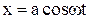 ,
, 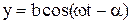 .
.
Проведемо очевидну послідовність операцій виключення параметра t:
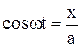 ,
, 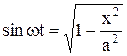 ,
, 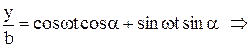
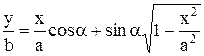 ,
, 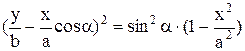
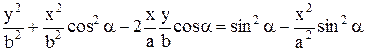
i, остаточно, маємо рівняння траєкторії, яку описує точка, у вигляді:
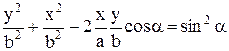
Одержане рівняння в загальному випадку є рівнянням кривої другого порядку. Розглянемо декілька прикладів:
а) Якщо різниця фаз коливань a = p, то sinp=0, cosp=-1 i загальне рівняння є рівнянням прямої:
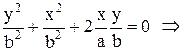
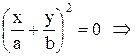
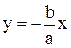 .
.
б) Якщо різниця фаз коливань a = 0, то sin0=0, cos0=1 i загальне рівняння є рівнянням прямої:
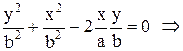
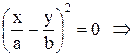
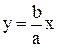
в). Якщо різниця фаз коливань a = 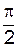 , то sin
, то sin 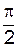 =1, cos
=1, cos 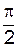 =0 i загальне рівняння є рівнянням еліпса:
=0 i загальне рівняння є рівнянням еліпса:
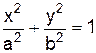
з напівосями а та b.
Биття
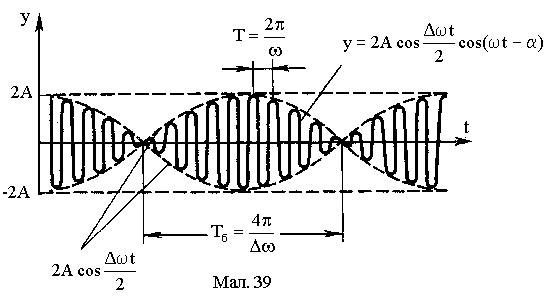 |
При взаємодії двох коливань із близькими значеннями частот w спостерігається періодична зміна амплітуди результуючого коливання (див.Мал.39). Це явище називається биттям. Нехай взаємодіють дві хвилі з частотами
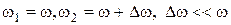 , рівняння яких має вид
, рівняння яких має вид
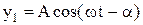 , (1)
, (1)
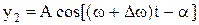 , (2)
, (2)
Результуюче коливання знайдемо у такий спосіб
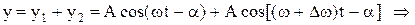
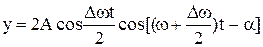 . (3)
. (3)
В (3) знехтуємо доданком 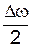 у виразі
у виразі 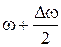 і одержимо
і одержимо
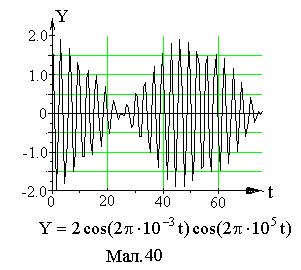
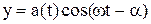 , (4)
, (4)
де амплітуда результуючого коливання а(t) має вигляд

Величина а(t) повільно змінюється з часом - її період 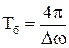 >
> 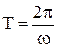 . Частота
. Частота 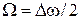 називається циклічною частотою биття.
називається циклічною частотою биття.
На Мал.40 представлена суперпозиція двох близьких за частотами коливань з Dw=4p×10-2 рад/с і w=2p×105 рад/с.
4.11. Контрольні питання
1. Дайте визначення коливального руху
2. Який рух називається періодичним
3. Дайте визначення гармонічного коливання
4. Дайте визначення пружної й квазипружної сили
5. Запишіть рівняння гармонічних коливань у комплексній формі
6. Дайте визначення пружинного маятника
7. Запишіть рівняння другого закону Ньютона для пружинного маятника
8. Запишіть диференціальне рівняння коливань для пружинного маятника у канонічній формі
9. Дайте визначення математичного маятника
10. Запишіть рівняння другого закону Ньютона для математичного маятника
11. Який фізичний зміст малих коливань математичного маятника
12. Запишіть диференціальне рівняння вимушених коливань математичного маятника в канонічному вигляді
13. Дайте визначення фізичного маятника
14. Запишіть рівняння другого закону Ньютона для фізичного маятника
15. Запишіть диференціальне рівняння вимушених коливань фізичного маятника в канонічному вигляді
16. Дайте визначення крутильного маятника
17. Запишіть диференціальне рівняння вимушених коливань крутильного маятника в канонічному вигляді
18. Дайте визначення вільних незгасаючих коливань
19. Розв¢жіть диферекціальне рівняння вільних незгасаючих коливань
20. Дайте визначення амплітуди, фази та початкової фази коливання
21. Дайте визначення власної частоти та визначіть період гармонічного коливання
22. Знайдіть швидкість та прискорення гармонічного коливання
23. Знайдіть кінетичну, потенціальну та повну механічну енергію гармонічного коливання
24. Дайте визначення вільних згасаючих коливань
25. Розв¢жіть диферекціальне рівняння вільних згасаючих коливань
26. Визначте аперіодичний рух
27. Визначте коливальний рух
28. Визначте частоту вільних згасаючих коливань
29. Визначте час релаксації
30. Визначте декремент та логарифмічний декремент згасання
31. Визначте добротність коливальної системи
32. Визначте вимушені коливання маятника
33. Визначте механічний резонанс та резонансну частоту
34. У чому полягає метод векторної діаграми
35. Визначте когерентні коливання
36. Визначте результат додавання двох когерентних гармонічних коливань
37. Знайдіть траєкторію руху точки, що здійснює взаємно перпендикулярні гармонічного коливання
38. Визначтебиття та виведіть рівняння і період биття
Дата добавления: 2015-09-18; просмотров: 3003;
