Класична модель розрахунку густини струму

З класичної точки зору, густина струму j лінійно залежить від концентрації носіїв струму n, величини заряду e та середньої швидкості направленого руху 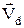і дорівнює

.

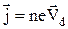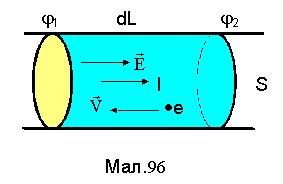
Дійсно, нехай у провіднику під дією напруженості електричного поля Е протікає струм І (див.Мал.96). Покладемо, що величина середньої швидкості направленого руху носіїв струму (дрейфова швидкість) є 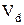. Через поперечний переріз провідника 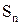(перпендикулярний до 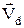) за час dt пройдуть всі електрони, які знаходяться на відстані dL= 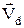dt від нього, тобто всі електрони, що знаходяться в об'ємі циліндра .

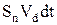Якщо концентрація електронів у провіднику n, то число цих електронів буде

,

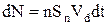а заряд, який вони перенесуть

.

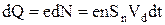Сила струму при цьому дорівнює

,

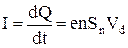а густина струму

,

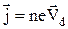що й треба було довести.

Зауважимо, що густина носіїв струму n у провідниках є сталою величиною.

10.3.Класична теорія електропровідності провідника.

10.3.1.Закон Ома у диференціальній формі

Класична модель електропровідності металів виходить із того, що під дією сили зовнішнього електричного поля 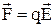, заряд q із масою m у проміжках між співударяннями з центрами розсіювання, наприклад, вузлами кристалічної решітки провідника, рухається прямолінійно з прискоренням 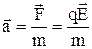. Приймається також, що час руху t між співударяннями електронів із вузлами решітки визначається їх довжиною вільного пробігу l і середньою тепловою швидкістю V_т

t = 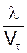. (1)

За цей час заряд набуває максимальну швидкість

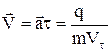. (2)

При цьому середня швидкість напрямленого руху носіївструму 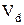приймається рівною середній швидкості рівноприскореного руху і вона дорівнює середній арифметичній від початкової V₀ і кінцевої швидкості V (у нашому випадку V₀ = 0)

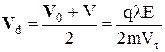. (3)

З іншого боку, експериментально визначено, що дрейфова швидкість пропорційна величині напруженості поля в провіднику

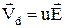, (4)

де коефіцієнт пропорційності u називається рухливістю носіїв струму. Підставивши в (4) значення V_д, знайдемо, що

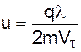. (5)

Тепер вираз j=neV можна записати у вигляді

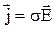, (6)

де коефіцієнт s називається провідністю і він дорівнює

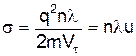. (7)

Провідністьs чисельно дорівнює густині струму при одиничній напруженості поля у провіднику, а вираз (6) має назву диференціального закону Ома.

Визначення провідності 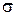, є змістом класичної теорії електропровідності провідників.

10.3.2.Закон Ома в інтегральній формі

З диференціального закону Ома можна безпосередньо одержати інтегральний закон. Для цього помножимо скалярно ліву та праву частини виразу 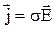на елементарну довжину провідника 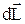(переміщення носія струму), утворивши співвідношення

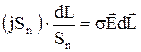. (1)

В (1) j×S_n=І є величина сили струму. Проінтегруємо (1) по ділянці кола L із точки 1 до точки 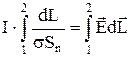2

. (2)

В (2) вираз

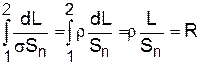(3)

є опір провідника, а 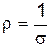¾ питомий опір. Інтеграл у правій частині (2) є напруга U на кінцях ділянки

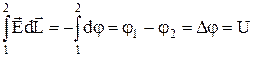. (4)

Остаточно з (2)-(4) маємо вираз для закону Ома в інтегральній формі

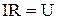, (5)

який він установив експериментально.