Геометричні тіла

Геометричним тілом називають частину простору обмежену сукупністю поверхонь і площин. Необхідною умовою існування геометричного тіла є відсутність розривів між утворюючими це тіло елементами. Вважається, що геометричні тіла заповнені деяким матеріалом, тому, при умовних розсіченнях їх прийнято штрихувати як штрихують метал – тонкими суцільними лініями з нахилом уліво або вправо під кутом 45º до горизонту.

Серед геометричних тіл є багатогранники, обмежені тільки плоскими багатокутниками, а так само велика кількість інших видів, що включають як поверхні, так і площини в різних сполученнях. Є поверхні, які без яких-небудь доповнень відносяться до геометричних тіл, тому що вони обмежують деякий обсяг простору. Найвідомішими є сфера, тор, еліпсоїд обертання і т.ін.

Типовими представниками багатогранників, в основі яких лежать пірамідальні й призматичні поверхні, є піраміди й призми.

Піраміда-багатогранник, у підставі якого лежить багатокутник, а бічні грані – трикутники із загальною вершиною.

Призма – багатогранник, у якого підстави – два однакових і взаємно паралельних багатокутники, а бічні грані – паралелограми. Якщо ребра призми перпендикулярні площинам підстави, то її називають прямою, якщо ні, то – похилою.

Площини, що створюють багатогранник, перетинаючись між собою, дають ребра й вершини багатогранника. Сукупність ребер і вершин прийнято називати сіткою багатогранника. Зображення багатогранника на кресленні зводиться до зображення його сітки.

Геометричні тіла, що включають поверхні, зображуються на кресленні крайніми (нарисовими) лініями. Якщо це поверхня обертання, то на її зображеннях обов'язкова присутність проекцій осей обертання.

Прямі кругові циліндр і конус утворюються з відповідних поверхонь обертання із залученням площин, перпендикулярних осі обертання. Ці площини носять назву підстав. Циліндр має дві підстави, а конус – одну, а також вершину. Усічений конус має дві підстави.

При зображеннях геометричних тіл часто виникає необхідність у перевірці на кресленні наявності об'єму тіла й визначення видимості окремих його елементів. Рішення таких завдань розглянемо на прикладі багатогранника (рис. 2.1).

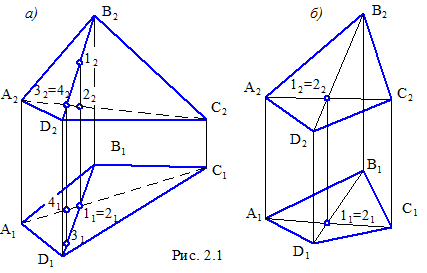У загальному випадку проекція багатогранника на площину представляє багатокутник у середині якого можуть бути (або не бути) відрізки прямих. Якщо вершини багатогранника позначені буквами (символізоване креслення), то двох проекцій досить для визначення взаємного положення його елементів, а так само їхнього положення щодо площин проекцій.

Виберемо дві конкуруючі точки, що лежать на ребрах DB і АС, проекції яких збігаються на площині П₁ (рис. 2.1, а). На фронтальній площині проекцій точка 1 розташовується вище точки 2, отже, ребро DB, якому належить точка 1, на площині П₁ буде видимим. У такий само спосіб визначається видимість на площині П₂. Збіг точок, що лежать на різних ребрах (рис. 2.1, б), говорить про те, що на кресленні замість багатогранника присутній плоский багатокутник.

При перерізах геометричних тіл площинами одержують замкнуту плоску фігуру, тому що в перетинах можуть брати участь площини й поверхні, що становлять поверхню цього тіла.

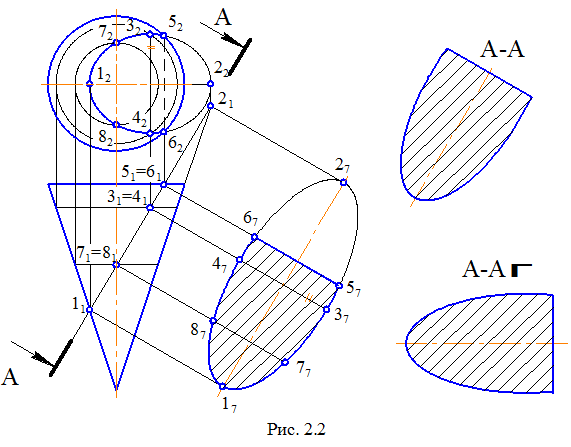На рис. 2.2 показана побудова лінії перерізу прямого кругового конуса із фронтальною підставою, горизонтально-проекціюючою площиною. Попутно введемо позначення розташування слідів-проекцій січної площини, прийняте на виробничих кресленнях. Це два штрихи розімкнутої лінії й стрілки, розташовані перпендикулярно цим штрихам, що вказують напрямок погляду при проектуванні. Позначають січну площину, а так само отриманий переріз, прописними літерами українського алфавіту. Незалежно від розташування січної площини ці літери розташовують горизонтально.

Переріз представляє плоску замкнуту фігуру, обмежену частиною еліпса і відрізком прямої. Він побудований за допомогою опорних точок, що належать січній площині, поверхні конуса й площині його підстави. Для зручності побудов узята точка 2. Вона не належить перетину, але визначає величину великої осі еліпса. Мала вісь (3, 4) розташована посередині великої осі під кутом 90º до неї. Вимір висот для побудови точок на перетині проводилось від горизонтальної осі симетрії фронтальної проекції конуса.

Перерізи широко використаються на виробничих кресленнях, найчастіше для пояснення форми окремих елементів деталі. Перерізом називають зображення фігури, одержуваної при уявному розсіченні предмета однієї або декількома площинами.

Переріз може бути повернений стосовно розташування січної площини. Повертають його на кут менший 90º, так щоб вісь розташовувалася горизонтально, і напис при цьому супроводжується особливим значком.

В утворенні лінії взаємного перетину геометричних тіл можуть брати участь всі елементи, що створюють ці тіла. 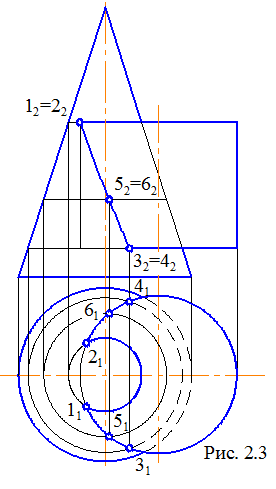Так, на рис. 2.3 бічна поверхня прямого кругового конуса перетинається не тільки з бічною поверхнею прямого кругового циліндра, але й з двома його підставами, що займають горизонтальне положення. Тому, аналізуючи розташування й характер лінії перетину, варто врахувати, що частина її горизонтальної проекції (ділянки 1₁5₁3₁ і 2₁6₁4₁) лежить на сліді-проекції циліндричної поверхні. На фронтальній площині проекцій так само є ділянки, що збігаються зі слідами-проекціями площин підстав циліндра. На площину П₁ вони проектуються неспотворено, дугами окружностей. Аналіз вимагає глибокого засвоєння навчального матеріалу глави 1.

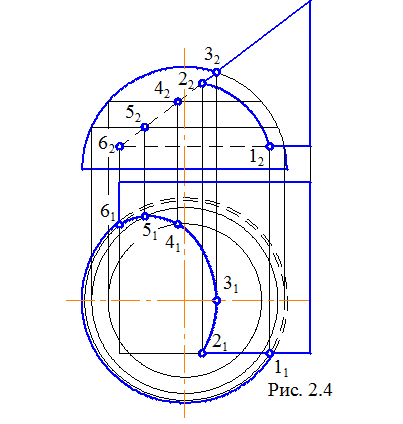
Ще один приклад побудови проекцій лінії взаємного перетину геометричних тіл (рис. 2.4).

Одне геометричне тіло представляє собою пряму призму, підставами якої є прямокутні трикутники фронтального положення. Другим геометричним тілом є півсфера. Лінія взаємного перетину складається з декількох дуг окружностей: переріз сферичної поверхні з фронтально-проекціюючою гранню (на П₁ зображується частиною еліпса), з горизонтальною гранню (частина окружності, що проектується неспотворено на П₁) і з фронтальною гранню (частина окружності, що неспотворено проектується на П₂).

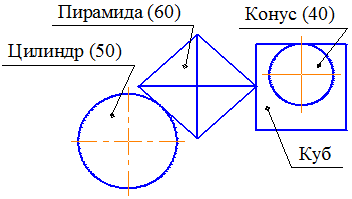◊ На рисунку представлено вид зверху групи геометричних тіл. Висота кожного тіла (у міліметрах) задана на кресленні в дужках. Циліндр, піраміда й куб своїми підставами розташовані на горизонтальній площині проекцій. Конус стоїть на кубі. Побудувати види спереду й справа цієї групи тіл, урахувати видимість.