ПОИСК ВЗАИМОСВЯЗЕЙ МЕЖДУ ПЕРЕМЕННЫМИ
Перекрестная группировка по двум и более признакам — прямой путь к обнаружению возможных связей взаимодействия между переменными. Для этого нужно составить таблицу определенным образом, например, подсчитать пропорции частот одного признака в зависимости от частот другого.
Правила процентирования — вовсе не так просты, как может показаться неопытному исследователю. Основной вопрос: принимать ли за 100% данные по строке или по столбцу? Это зависит от двух обстоятельств: от характера выборки обследованных и от логики анализа. Выборка может быть либо репрезентативной (выборочная совокупность есть микромодель генеральной совокупности), либо нерепрезентативной. В последнем случае нам как минимум неизвестны пропорции существенных характеристик в генеральной совокупности, или мы знаем, что эти пропорции в выборке не соблюдаются. Возможна двоякая логика анализа "от причин к следствию" или "от следствий к причинам", что определяется гипотезой и содержанием данных.
Если выборка представительна и отражает пропорции изучаемых групп в генеральной совокупности (данного завода, например), тогда можно вести двоякий анализ данных: по логике "от причин к следствию" и "от следствия к причинам ".
Рассмотрим пример. Предположим, что 1000 человек, работающих на заводе, распределились в зависимости от того, участвуют или не участвуют они в рационализации, следующим образом (табл. 10).
Проведем анализ по логике: "от возможных причин - к следствию". Предпосылкой более или менее активного участия в рационализации может быть содержание труда, тогда как рационализаторство само по себе не может быть причиной того или иного вида профессионального труда, это - возможное следствие первого фактора. При таком подходе за 100% следует брать данные по строке (табл. 10а).
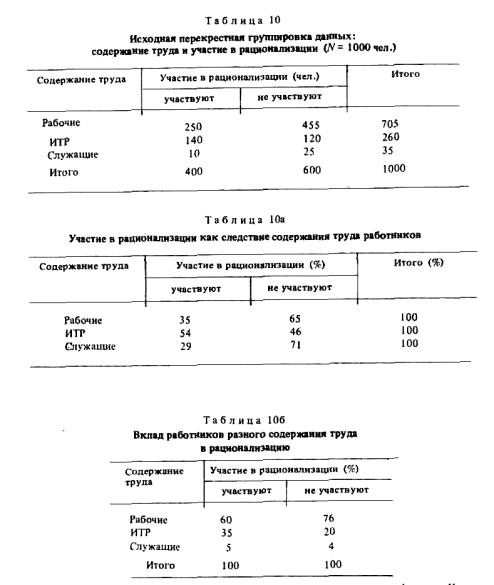
Вывод: наиболее активные рационализаторы - ИТР, наименее активные - служащие. Характер труда инженерно-технических работников способствует участию в рационализации в большей мере, чем характер труда служащих или рабочих данного предприятия.
Теперь проведем анализ по логике "от следствия к причинам": 100% суммируются в столбце (табл. 10 б).
С логической точки зрения здесь проверяется гипотеза о вкладе каждой категории работников в рационализаторское движение, а не гипотеза об их соотносительной рационализаторской активности. Вывод из табл. 10 б: вклад рабочих — наибольший, так как они преобладают в числе сотрудников предприятия. Об относительной же активности рабочих по этим расчетам мы судить не можем.
Итак, ретроспективный и проектирующий анализы предполагают различные по содержанию выводы.
В репрезентативных выборках возможно процентирование "по диагонали" таблицы. Например, для табл. 6 (если данные представительны) можно подсчитать процентные доли всех 47 выделенных в ней сочетаний возрастных характеристик мужей и жен, из чего, скажем, следует, что более всего в изученной совокупности представлены молодые пары в возрасте 20—24 лет, каковые составляют около 55% от всех пар
(504 : ——— = 0,55),
среди 50-летних и старше супружеские пары одного возраста составляют лишь 5% и т.д.
Если выборка нерепрезентативна, процентирование можно вести только в рамках каждой подвыборки раздельно. Обычно такие подвыборки образуют по признакам, являющимся возможными причинами искомых связей: половозрастные, профессионально-квалификационные, группы по уровню образования, другим объективным характеристикам социального статуса, места проживания и т.д. Здесь несоответствие долей подвыборок реальному распределению выделенных групп в генеральной совокупности не исказит вывод (логика табл. 10 а). В противном же случае (по логике табл. 106) достоверность вывода будет прямо зависеть от уровня представительности выборки.
Наконец, в случаях, когда представительность перекрестной классификации в принципе нельзя установить (например, при совмещении данных об удовлетворенности условиями труда и быта, где распределение в генеральной совокупности заранее вообще неизвестно), расчет процентов допустим в обоих направлениях и по диагонали с условием, что установленные связи требуют дополнительной проверки, ориентировочны. Для такой проверки используют систему так называемых контрольных (промежуточных) переменных.
Анализ взаимосвязи двух переменных с помощью контрольного фактора — прием, используемый для того, чтобы установить прямые и опосредованные, причинные и сопутствующие связи, а также уточнить их напряженность. Рассмотрим три вымышленных примера, в которых проиллюстрируем основные логические проблемы этого метода.
Пример первый. Надо определить, имеется ли связь между интересом людей к познавательным программам телевидения (обозначим как фактор П) и к развлекательным программам (фактор Р).
Для установления взаимосвязи между этими явлениями используем простейший показатель — коэффициент ассоциации двух качественных переменных по Юлу. Чтобы подсчитать коэффициент ассоциации Юла, достаточно фиксировать наличие ( + ) или отсутствие ( — ) каждого из двух сопоставляемых качеств А и В.
Построим двумерную классификационную таблицу (схема 25).
Связи между признаками П и Р в производных таблицах, выравненных по образованию, не обнаружено. Между тем в исходной табл. 11 связь высокая. Остается предположить, что и П и Р зависят от уровня образования, но независимы относительно друг друга. Проверим это предположение, сгруппировав данные так, чтобы выявить связи между контрольным фактором (О - образование) и каждым из первоначальных ( П и Р) (табл. 11 б).

Видно, что связь между образованием и интересом к программам познавательных передач так же, как между образованием и интересом к развлекательным программам, высока:

Здесь действует следующее правило: если введение контрольной переменной уменьшает связь между двумя исходными переменными, но связь между контрольной переменной и каждой из исходных достаточно высока, контрольная переменная выступает либо в качестве интерпретирующей, либо в качестве объясняющей. Различие же между интерпретацией и объяснением состоит в следующем. Интерпретация — способ истолкования факторов, рассматриваемых как посредствующие переменные какого-то процесса, причины которого неясны. Объяснение суть истолкование ряда факторов, рассматриваемых в качестве причинных переменных.
Чтобы иллюстрировать метод обнаружения интерпретирующей и объясняющей связи, рассмотрим другой пример, используя ту же логику рассуждения и те же цифровые данные.
Пример второй. Обозначим Пр профессию телезрителей (Пр1 и Пр2 — это две группы профессий), И+ наличие И‾ отсутствие интереса к определенным программам. Для таблицы ПрИ, используя те же данные, что в табл. 11, связь равняется 0,82 по коэффициенту ассоциации Юла QПрИ = 0,82).
Введем контрольную переменную О - образование. Перестроив таблицы, как в предыдущем случае, найдем, что в производных связь потерялась: при фиксированном уровне образования не обнаруживается связи между профессией и интересом к передачам определенного типа. Иначе говоря, люди с высшим образованием — инженеры, врачи, учителя - примерно одинаково интересуются передачами данного класса. Рабочие, продавцы магазинов, служащие учреждений, не имеющие высшего образования, также обнаруживают большую схожесть в отношении к телепрограммам этого класса.
Как и в предыдущем случае, введение контрольной переменной снизило (или в нашем условном примере свело к нулю) связь между исходными факторами. Однако заключение во втором случае будет отличаться от вывода, который следует из первого примера.
В первом примере образование предшествует интересу телезрителей к развлекательным или образовательным программам и потому объясняет связи так: между интересом к развлекательным и образовательным программам существует связь сопутствия, ибо, не будучи прямо связанными между собой, обе эти разновидности интересов связаны с третьим фактором — образованием, которое и является причиной переменной.
Логика объяснений связей между П и Р через О:
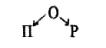
Во втором примере контрольная переменная (образование) не предшествует, но действует одновременно с одной из основных переменных (профессия). В этом случае она опосредует связь между основными факторами и уточняет, интерпретирует ее: дело не столько в профессии, сколько в образовании.
Логика интерпретации связи между Пр и И через О:
Пр ® О ® И.
Пример третий. Возможна ситуация, когда связь между двумя исходными переменными после введения контрольной не исчезает и не уменьшается, но она исчезает между одной из исходных переменных и контрольной. Рассмотрим этот вариант на условном примере с телезрителями.
А — интерес телезрителей к программам "Что, где, когда?"; В — их интерес к программам "В мире животных". Контрольная переменная (О) — образование.
Имеем серию из трех типов таблиц: исходная, промежуточные и итоговая. Первичная связь такова.

Между интересом к передачам "Что, где, когда?" и "В мире животных" есть незначительная связь в пользу второй (Q = - 0,20). Введем контрольную — образование (табл. 12а).

Связь усиливается: люди с высоким образованием проявляют больший интерес к передачам "Что, где, когда?", люди с низким образованием больше интересуются циклом "В мире животных".
Перестроив таблицы, рассмотрим теперь связи между образованием и интересом к двум типам передач последовательно (табл. 126).

Оказывается, что связи между образованием и интересом к программам "Что, где, когда?" (фактор А) нет: люди смотрят или не смотрят эти программы независимо от уровня образования. Здесь действуют какие-то иные факторы, помимо образования. Правда, есть незначительная связь между уровнем образования и интересом к передачам "В мире животных" (фактор В).
Этот тип анализа можно назвать спецификацией, или уточнением, в отличие от анализа по логике объяснения, или интерпретации.
Во всех рассмотренных примерах мы имели дело с тремя переменными. Однако их могло бы быть и больше. Логика анализа при этом остается прежней, меняется лишь численность промежуточных членов в порядке анализа вследствие добавления новых контрольных факторов. Аналогична стратегия поиска взаимосвязей между более чем тремя, притом не дихотомическими, а многочленными качественными или количественными, переменными. Принципиальное отличие — в технике анализа.
Вместо измерения ассоциации двух переменных с помощью критерия Юла устанавливаются многофакторные функциональные связи (корреляции) и связи детерминации (регрессионный анализ). Приемы такого анализа рассматриваются в специальной литературе по статистике и математическим методам в социологии [см., напр., 86, 147, 183, 246, 275].
Исследование многомерных взаимосвязей и взаимозависимостей — типичная задача в социологии. Как правило, такие зависимости не удается "схватить" сразу каким-то единственным математическим методом. Прибегают к различным средствам анализа в поисках наиболее "наглядного", убедительного отображения. Один из широко используемых сегодня способов такого рода — метод отображения взаимосвязей в корреляционном графе, предложенный эстонским математиком Л. Выханду [55].
Граф — это фигура, состоящая из точек (их называют вершинами графа) и отрезков, соединяющих некоторые из этих точек (ребра графа). О графе мы уже упоминали, рассматривая социометрические процедуры. Изображение связей в группе с помощью социограммы есть граф (рис. 12, с. 178). В социограмме указываются вершины графа (члены группы) и связи между ними (ребра графа).
Если бы удалось измерить корреляции или тесноту связей между всеми членами группы (вершинами) и соответственно этому выделить наиболее близкие и наиболее отдаленные связи, такое изображение можно было бы назвать корреляционным графом.
Чтобы построить корреляционный граф, измеряют парные связи между всеми переменными, обозначенными на графе как его вершины. Например, имея пять переменных А, В, С, D и Е, покажем, как связана каждая из них с каждой другой в матрице интеркорреляций (табл. 13).
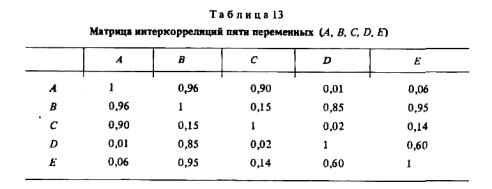
Связи между выделенными переменными можно описать графом, изображенном на рис. 16.
Между вершинами А, В и С существуют взаимосвязи RBA = 0,96; RAC = 0,90; RBC = 0,15. Связь RBC можно опустить, так как она намного слабее ("длиннее"), чем связь С и В через вершину А.
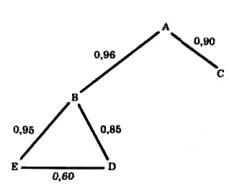
Рис.16. Корреляционный граф по методу Выханду
Иными словами, переменная А является для В и С либо объясняющей, либо интерпретирующей (В и С связаны как сопутствующие).
Иная связь между вершинами В, D и Е. Все они взаимодействуют на уровне R более 0,60. Но каждая из них связана с вершиной С очень слабо (от 0,02 до 0,14). В является промежуточной между А, с одной стороны, Е и D — с другой так как связи Е с А гораздо слабее, чем их связи с В, которая, в свою очередь, тесно связана с А.
В корреляционном графе отображаются лишь те связи между вершинами, которые соединяют их кратчайшим путем (т.е. являются наиболее тесными), и опускаются другие, менее тесные связи. На языке теории графов [36] это означает, что мы разрываем замкнутые дуги и оставляем только те ребра, которые связывают вершины наиболее тесно.
С помощью методов факторного анализа выявляют структурные взаимосвязи множества переменных [93, 136,138,140, 197].Сначала устанавливаются парные корреляции всех изучаемых переменных, а затем отыскиваются своего рода корреляционные плеяды или "узлы" связей. Иными словами, выделяют такие переменные, которые, будучи наиболее тесно взаимосвязаны в рамках своей плеяды, слабо связаны с другими корреляционными узлами. Выявленные "узлы" и есть факторы. Название фактора всегда условно и подбирается по ассоциации с теми переменными, которые наиболее сильно связаны с данным фактором — имеют наибольшие "факторные нагрузки".
Приведем пример (табл. 14) из нашего исследования отношения рабочих к труду (1976 г., Ленинград), в котором факторному анализу подвергнуты оценки удовлетворенности различными элементами производственной ситуации (более 4 тысяч рабочих разного характера труда) [220, с. 146-147].
Из табл. 14 видно, что первый фактор до вращения вобрал в себя с положительными значениями все изучаемые связи, исчерпав почти четверть их вариации. Это показатель "силы" фактора, его информативности, равной в данном случае 23,4%. Наиболее значимы в данном факторе оценки организации труда (0,707), состояния оборудования (0,609), отношений с администрацией (0,647), техники безопасности (0,653), а наименьшие связи обнаруживают оценки содержательных аспектов работы: ее разнообразия (0,213), возможности проявить смекалку (0,272) и т.п. Так как в генеральном факторе все изучаемые признаки взаимосвязаны, его можно назвать фактором общей удовлетворенности, в котором лидируют оценки условий труда.
Второй фактор, сила которого в два раза меньше (информативность) 12,8%) - биполярный: одни оценки вошли в него с положительными значениями (содержательные аспекты работы, например разнообразие, возможность проявить смекалку), а другие (условия труда) — с отрицательными.
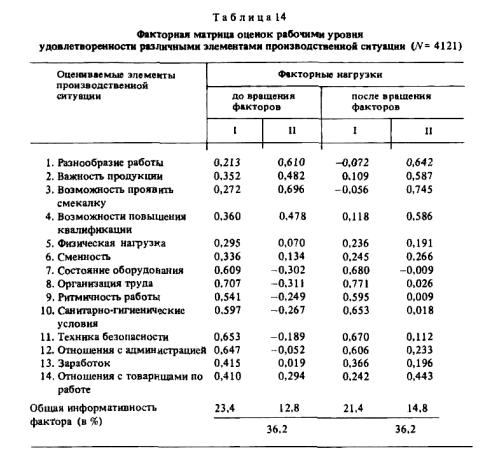
Это указание на то, что имеются две подструктуры связей, которые могут быть прояснены операцией вращения факторов.
После вращения четко обозначились две структурные составляющие: 1-й фактор (достаточно информативный = 21,4%) - фактор условий труда, так как в нем с высокими положительными нагрузками присутствуют оценки удовлетворенности именно условиями труда. 2-й фактор (14,8%) - фактор удовлетворенности содержательными аспектами работы. При этом в рамках отношения к содержанию труда лидирует творческий аспект - возможность проявить смекалку (0,745), отношение к разнообразию работы (0,642), удовлетворенность тем, насколько важна выпускаемая продукция (0,587), каковы возможности повышения квалификации (0,586). Во втором факторе особо важны организация труда, состояние оборудования, санитарно-гигиенические условия, ритмичность работы и некоторые другие (все с весами около 0,6).
Далее, на основе обнаружения этих двух структур (их может быть больше, если мы продолжим извлечение факторов, т.е. начнем разукрупнять факторную модель на более дробные составляющие) каждому обследованному могут быть приписаны "веса" по двум показателям (двум факторам): удовлетворенности условиями и содержанием труда. Теперь мы знаем, какой соотносительный "вес" имеет в этих двух факторах оценка каждого частного элемента производственной ситуации. Мы знаем также индивидуальную оценку данным рабочим каждого из элементов производственной ситуации и путем несложных арифметических действий можем приписать всем обследованным "персональные индексы" удовлетворенности условиями и содержанием труда более обоснованно, чем это было бы сделано без использования факторного анализа.
Таким образом, факторный анализ позволяет взвесить значимость каждого из элементов производственной ситуации в обшей структуре оценок удовлетворенности и соответственно учесть эти поправки при расчетах интегральных индивидуальных показателей удовлетворенности условиями труда и содержанием труда, т.е. будут получены два обобщенных показателя на каждого обследуемого вместо 14 исходных.
Дата добавления: 2015-09-11; просмотров: 1128;
