Взаимное положение прямых. Как известно из программы средней школы, прямые могут пересекаться, быть параллельными (лежать в одной плоскости и не иметь общей точки) и скрещиваться

Как известно из программы средней школы, прямые могут пересекаться, быть параллельными (лежать в одной плоскости и не иметь общей точки) и скрещиваться (лежать в разных плоскостях и не иметь общей точки).

На рисунке 12 изображен чертеж параллельных прямых – одноименные проекции двух параллельных прямых параллельны между собой.

Справедливо и обратное заключение, кроме случая с профильными прямыми. Если даны профильные прямые, то их параллельность проверяется по профильным проекциям.

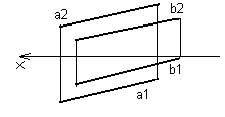
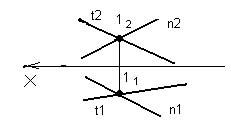
Рисунок 12 Рисунок 13

На рисунке 13 изображены пересекающиеся прямые t (t1, t2) и n (n1, n2). Чертеж пересекающихся прямых показывает, что если прямые пересекаются, то их одноименные проекции пересекаются между собой, а проекции точки пересечения лежат на одной линии связи.

Скрещивающиеся прямые – прямые, которые не пересекаются и не параллельны между собой. На эпюре скрещивающиеся прямые будут напоминать пересекающиеся с той лишь разницей, что точки пересечения фронтальных и горизонтальных проекций не будут лежать на одной линии связи (перпендикуляре к оси ОХ), рисунок 14. В связи с этим вводится понятие конкурирующие точки.

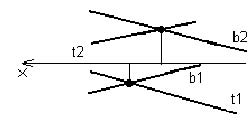
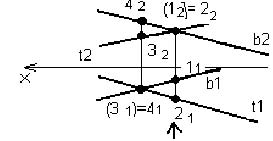
Рисунок 14 Рисунок 15

Точки, лежащие на одном проецирующем луче, называются конкурирующими.

На рисунке 15 обозначены конкурирующие точки и определена их видимость на П1 П2, невидимые точки берутся в скобки. Давайте рассмотрим подробно. На фронтальной проекции пересекаются фронтальные проекции прямых t2 и b2. Обозначим эту точку 1 с индексом 2 и 2 с индексом 2. Допустим, что в пространстве точка 1 лежит на прямой b, а точка 2 на прямой t. Обозначим в соответствии с этим горизонтальные проекции точек 1 и 2. Для определения видимости точек на фронтальной плоскости проекций нужно сравнить координаты Y точек 1 и 2. Координата Y (.) 2 > Y (.) 1, следовательно на фронтальной плоскости проекций точка 2 будет видимой, а точка 1 будет лежать на одном проецирующем луче с точкой 2 и окажется "прикрытой" точкой 2, т. е. невидимой глазу наблюдателя. Такие точки берутся в круглые скобки. На горизонтальной плоскости проекций пересекаются горизонтальные проекции прямых в точке, которую обозначим цифрой 3 с индексом 1 и цифрой 4 с индексом 1. Эти две точки в пространстве лежат на разных прямых, допустим точка 3 на прямой t, а точка 4 на прямой b. Обозначим соответственно этому допущению фронтальные проекции точек. Чтобы определить видимость точек на горизонтальной плоскости проекций нужно сравнить координаты Z этих точек. Координата Z (.) 4 > Z (.) 3, следовательно, на горизонтальной плоскости проекций будет видна точка 4, а точка 3 будет находиться под ней, и ее нужно взять в скобки.

Контрольные вопросы

1. Какой координатой измеряется расстояние от заданной точки А до фронтальной плоскости проекций?

2. Какая прямая называется прямой общего положения?

3. Как располагаются проекции фронтальной прямой уровня, фронтально-проецирующей прямой?

4. Что называется следом прямой?

5. В какой плоскости проекций лежит горизонтальный след прямой?

6. Какой след отсутствует у профильной прямой уровня?

7. Какой плоскости проекций параллельна горизонтальную линию уровня?

8. Постройте эпюр фронтальной линии уровня, пересекающей ось ОY.

9. Каким плоскостям проекций параллельна профильно-проецирующая прямая?

10. На какие плоскости проекций отрезок фронтально-проецирующей прямой АВ проецируется в натуральную величину?

11. Какие точки называются конкурирующими?

12. Начертите эпюр пересекающихся прямых, точка пересечения которых имеет координаты (20, 30, 50).

13. Начертите на эпюре прямую, пересекающую ось ОХ в точке С(25, 0, 0).