Двухступенчатые триггеры

Триггеры с двухступенчатым запоминанием информа­ции состоят из двух триггерных структур. Одна называет­ся ведущий триггер, другая — ведомый триггер (рис. 3.16)

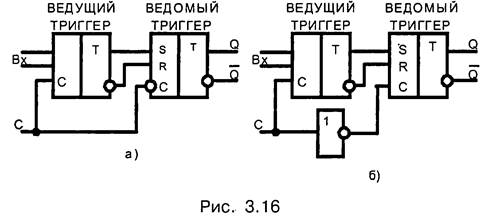
Оба триггера — синхронные, но имеют противополож­ные синхровходы. На рис. 3.16 ведущий триггер срабаты­вает при С = 1, имеет прямой синхронизирующий вход, а ведомый при С = 0 — инверсный синхронизирующий вход.

На первом этапе, когда происходит запись информа­ции в ведущий триггер, ведомый отключен, продолжает сохранять предыдущее состояние. Когда снят активный уровень с синхровхода ведущего триггера, происходит перезапись информации в ведомый триггер. Таким обра­зом, происходит поэтапная запись информации благодаря управлению инверсными логическими уровнями.

В двухступенчатом триггере устраняется противоречие между процессами хранения старой и приема новой ин­формации. Это дает возможность построения синхронных автоматов без опасных временных состояний, исключить предпосылки к режиму генерации. Позволяет обеспечить высокую надежность функционирования триггеров с внут­ренними цепями обратной связи. В то же время схемы этих триггеров более сложные, чем схемы триггеров с ди­намическим входом, а быстродействие ниже.

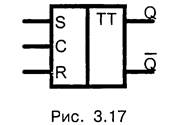Часто двухступенчатый триггер называют MS-тригге­ром от английских слов «master» и «slave» — хозяин и раб. На принципиальных схемах двухступенчатые триг­геры обозначаются сдвоенной буквой (ТТ) рис. 3.17.

JK-триггер

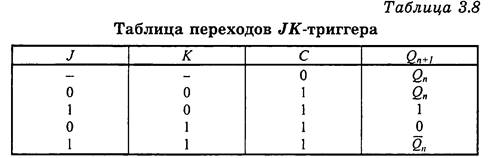
JK-триггеры — это двухступенчатые универсальные синхронные триггеры. Универсальность заключается в том, что на их основе можно сделать любой другой тип логи­ческих триггеров RS, D, Т. Вход J аналогичен входу S уже рассмотренного RS- триггера, т.е. устанавливает в единичное состояние Q=1 при J=1.Вход К устанавливает JK-триггер в нулевое состояние, т. е. аналогичен входу R: Q = 0 при К = 1.

Отличие от RS-триггера заключается в том, что JK- триггер не имеет запрещенных входных комбинаций. Если на оба входа J и К подать активный логический уровень, то триггер перейдет в состояние, противоположное пре­дыдущему: Q_n+1= 0, при J = К = 1.

Входной сигнал зависит не только от состояния вход­ных сигналов, но и от предыдущего состояния JK-тригге­ра.

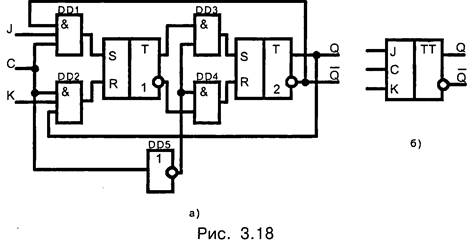
На основе JK-триггера может быть построен любой другой триггер (рис. 3.19). На рис. 3.19, а — синхронный RS-триггер, на рис. 3.19, б — D-триггер, на рис. 3.19, в — синхронный Т-триггер, на рис. 3.19, г — асинхронный Т-триггер.

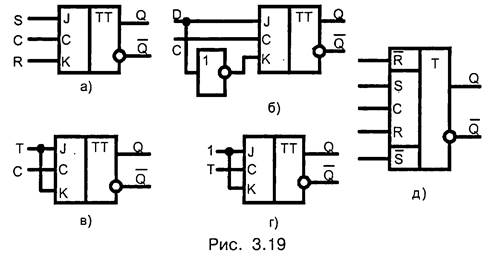
JK-триггер, как и другие типы триггеров, может допол­нительно иметь входы начальной установки (рис. 3.19, д), которые являются инверсными по отношению ко входам J, К.

JK-триггеры — это более сложные триггеры, содер­жат большее число элементов, поэтому потребляемая мощ­ность Р_пот оказывается большой. Меры, принимаемые к уменьшению потребляемой мощности, нередко приводят к ухудшению частотных свойств. JK-триггер вследствие своей универсальности и отсутствия запрещенных комби­наций находит широкое применение в цифровой технике.

Счетчики

Счетчиком называется последовательностное устрой­ство, предназначенное для счета входных импульсов и фиксации их числа. Счет импульсов является одной из наиболее распрост­раненных операций в устройствах дискретной обработки информации.

Основное функциональное назначение счетчиков:

1. счет импульсов, поступивших на вход;

2. деление частоты.

Из определения и логики работы счетчиков следует, что их текущее состояние зависит не только от нового пришедшего импульса, но также и от количества преды­дущих импульсов. Значит, счетчики относятся к устрой­ствам с памятью. Строятся счетчики на основе однотипных связанных между собой триггеров. Наи­более часто используются Т- и JK-триггеры. Ведь T-триггеры так и называются — счетные триггеры. С другой сто­роны в JK-триггерах обеспечивается смена состояния на противоположное предыдущему

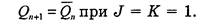
Комбинационные элементы в счетчиках используются для управления работой триггеров. Число триггеров опре­деляет максимальное количество импульсов, которое мо­жет быть подсчитано счетчиком.

В счетчиках выполняются следующие логические опе­рации:

1. установка в нулевое состояние (сброс);

2. запись входной информации в параллельной фор­ме — начального кода, с которого начинается счет;

3. хранение записанной информации;

4. выдача хранимой информации в параллельной форме;

5. инкремент — увеличение хранящегося числа на еди­ницу;

6. декремент — уменьшение хранящегося числа на еди­ницу.

Основным параметром счетчика является модуль сче­та М, равный максимальному числу импульсов, после которых счетчик устанавливается в исходное состояние (обнуляется) и начинается новый цикл работы счетчика.

По значению модуля счета различают:

· двоичные счетчики, модуль счета которых равен це­лой степени числа два M=2ⁿ, где n — число используемых триггеров;

· двоично-кодированные, в которых модуль счета мо­жет быть любом числом, не равным 2.

По направлению счета счетчики бывают:

· суммирующие (прямого счета), в которых происхо­дит увеличение состояния счетчика — инкремент;

· вычитающие (обратного счета), в которых состоя­ние счетчика уменьшается — декремент;

· реверсивные, которые по управляющему сигналу мо­гут как увеличивать, так и уменьшать свое состояние.

Как и все цифровые устройства, счетчики бывают син­хронные и асинхронные.

Быстродействие счетчиков характеризуется временем установления в нем нового состояния, а также максималь­ной частотой следования поступающих импульсов.

Отечественные микросхемы счетчики можно опреде­лить по маркировке функционального назначения буква­ми ИЕ, например, К555ИЕ2. На принципиальных схемах счетчики обозначаются буквами СТ2, СТ10.

По способу кодирования внутренних состояний разли­чают двоичные счетчики, счетчики Джонсона, счетчики с кодом «1 из N», счетчики в коде Грея и др. Наибольшее распространение получили двоичные счетчики, а из дво­ично-кодированных чаще всего применяют двоично-десятичные. Счетчики с другим модулем счета можно полу­чить путем введения дополнительных связей между раз­рядами.

Двоичные счетчики

Работу асинхронного счетчика рассмотрим на примере микросхемы К555ИЕ5 — четырехразрядного двоичного счетчика на двухступенчатых счетных триггерах. Этот счетчик имеет два счетных входа С1,С2 и два входа уста­новки нуля R0 (1), R0 (2) (рис. 3.40).

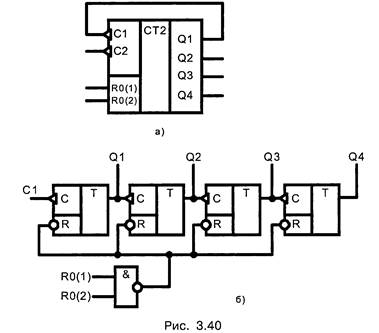
Триггеры срабатывают по срезу входного импульса (при переходе из 1 в 0). Четыре последовательно соединенных триггера образуют счетчик модулю 2⁴ = 16. Максимально хранимое в счетчике число полном его заполнении

N = 2⁴ - 1 = 15₁₀= 1111₂.

Из таблицы 3.16 и рис. 3.41 видно, что при срабатыва­нии по заднему фронту (срезу) триггеры имеют инверсные динамические входы. Состояние счетчика в двоичном коде по приходу на вход каждого нового импульса увеличива­ется на единицу, осуществляется операция инкремента.

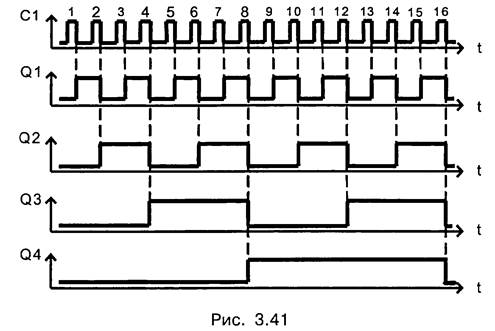
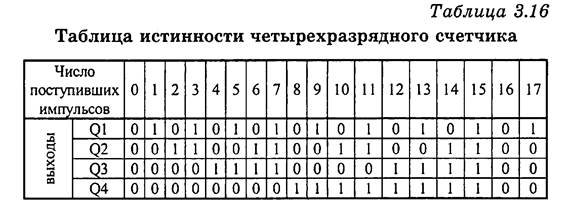
Так как счетный триггер делит частоту входных им­пульсов на два, то цепочка из четырех последовательно соединенных триггеров делит частоту на 16. По приходу каждого шестнадцатого импульса счетчик обнуляется и цикл счета начинается сначала.

Представленный на рис. 3.40 счетчик является сум­мирующим.

Если исходные асинхронные Т-триггеры имеют прямые динамические входы, срабатывают по переднему фронту импульса при переходе из 0 в 1, то счетчик превращается в вычитающий. Он выполняет операцию декремента. Времен­ные диаграммы такого счетчика приведены на рис. 3.42.

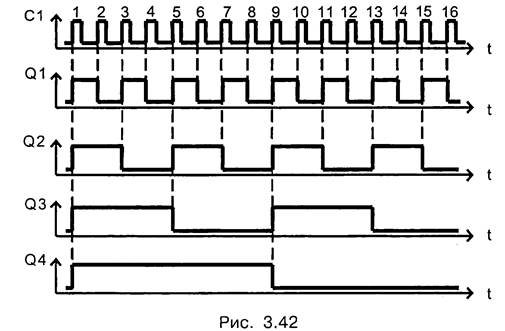
В обоих рассмотренных случаях для синхронизации каждого последующего асинхронного T-триггера исполь­зовался прямой выход предыдущего триггера Q. Если ко входам подключать инверсный выход Q, то суммирую­щим будет счетчик с прямыми динамическими входами.

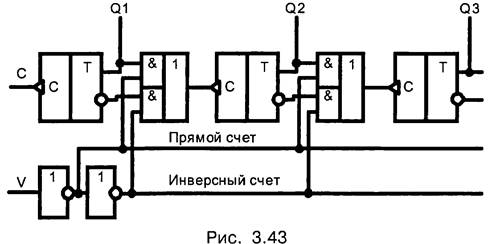
Используя различные варианты прямого и обратного счета, можно получить реверсивный счетчик. Такое пере­ключение осуществляется с использованием элементов И- ИЛИ, И-ИЛИ-НЕ, которые устанавливаются между триг­герами (рис. 3.43).

При поступлении на вход V логического нуля V = 0 на выходы верхних по схеме элементов И поступает логичес­кая единица и к инверсным динамическим входам триг­геров подключены прямые входы предыдущих триггеров. Счетчик выполняет операцию суммирования. При подаче сигнала V = 1 по входам триггеров (инверсным динами­ческим) подключается инверсный выход предыдущих триг­геров и выполняется операция вычитания.

На рис. 3.43 показан один из вариантов построения реверсивного счетчика. Возможны и другие варианты, использующие тот же самый принцип организации межразрядных связей.

В рассмотренных счетчиках при последовательном со­единении триггеров переключение каждого триггера мо­жет произойти только после переключения предыдущего. Поэтому они называются счетчиками с последовательным переносом. Такие счетчики отличаются простой схемой, но в то же время имеют наибольшее время установления выходного кода, которое к тому же является различным при различном состоянии счетчика. Например, если в счет­чике записаны числа 0₁₀ = 0000₂, 0100₂= 4₁₀, и т. д., то переключается только один триггер, а при переходе из состояния 15₁₀= 1111₂, либо 7₁₀ = 0111₂ переключаются все четыре триггера. Новый тактовый импульс можно по­давать на счетчик после того, когда установятся все триг­геры. Таким образом, период следования Т входных им­пульсов должен удовлетворять соотношению

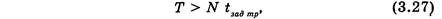
где N — число разрядов счетчика;

t_{3ad mp} — время задержки одного разряда.

Уменьшить время установления можно при условии, что все разряды счетчика будут переключаться одновре­менно. В этом cлучае следует отказаться от асинхронных счетчиков и перейти к использованию синхронных.

Из анализа таблицы 3.16 и рис. 3.41 для суммирую­щего асинхронного счетчика отметим: переключение каждого i-ro триггера происходит по приходу нового входного импульса при условии, что все предыдущие триггеры находятся в единичном состоянии. В этом слу­чае i—й триггер меняет свое состояние. Математически с помощью формул алгебры логики данный алгоритм записывается

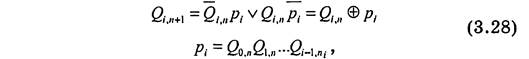
где p_t — сигнал переноса;

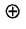— символ сложения по модулю два.

Из формул 3.28 следует, что сигнал переноса p_i форми­руется с помощью многовходовых элементов И. На рис. 3.44 представлен фрагмент схемы.

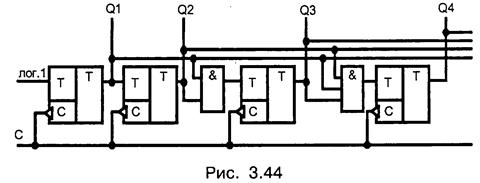
В схеме на рис. 3.44 все триггеры устанавливаются одновременно по приходу синхроимпульса С. Время уста­новки счетчика равно времени задержки в одном разряде. Счетчики, реализующие алгоритм (3.28), называются счет­чиками с параллельным переносом. Они имеют значитель­но более высокое быстродействие.

Повышение быстродействия достигается за счет услож­нения схемы. Время установления t_ycm таких счетчиков не зависит от числа разрядов и равно

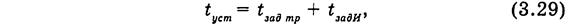
где t_3aдИ — время задержки элемента И.

Однако, с ростом числа разрядов реализация парал­лельных счетчиков вызывает затруднения. Растет число входов элементов И, растет нагрузка на выходы тригге­ров. Кроме того, одновременное переключение сразу мно­гих триггеров в счетчике создает значительный импульс тока в цепях питания.

Поэтому при большом числе разрядов используют ком­бинированную структуру последовательно — параллельно­го переноса. Суть данной организации состоит в объедине­нии нескольких триггеров в группы. Формирование сигна­ла переноса осуществляют между группами (рис. 3.45)

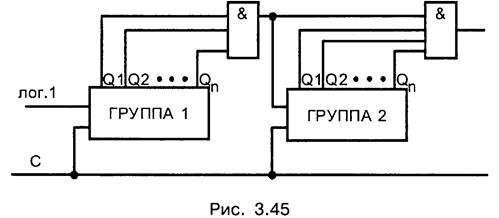
Сигнал переноса из группы триггеров возникает при условии, что все триггеры этой группы находятся в еди­ничном состоянии.

Упрощение комбинированного счетчика с последова­тельно- параллельным переносом приводит к некоторому снижению его быстродействия:

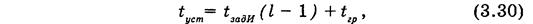
где l — число групп;

t — время задержки (установления) в группе.

При необходимости формирования счетчиков большой размерности и уменьшения импульсов тока при переклю­чении переходят к формированию счетчиков в коде Грея. Суть кода Грея заключается в том, что при переходе от одной кодовой комбинации к следующей соседней изме­няется состояние только одного разряда. Однако получен­ный результат затем необходимо перевести в двоичный код с использованием преобразователя кода.