Критическая частота вращения вала постоянного сечения с равномерно распределенной массой

Вал постоянного сечения с равномерно распределенной массой по длине (при 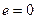) вращается, имея прогиб. Для определения его критической частоты воспользуемся дифференциальным уравнением колебаний призматического стержня, которое запишется в виде

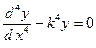(5.18)

где

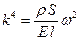. (5.19)

Здесь 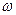- угловая скорость вращения; 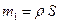- масса единицы длины вала.

Обще решение дифференциального уравнения (5.18), содержащее четыре произвольных постоянных, имеет вид

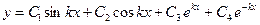. (5.20)

Учитывая граничные условия для вала, свободно лежащего на двух опорах, получаем систему однородных уравнений, при совместном решении которых определяются произвольные постоянные:

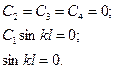(5.21)

Уравнение (5.21) удовлетворяется, если

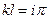(5.22)

где .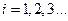

Из выражений (5.19) и (5.20) получим формулы для определения критической угловой скорости:

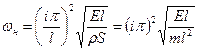, (5.23)

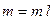где - масса единицы длины; - масса всего тела.

Окончательное уравнение упругой линии вала получаем из (5.20) при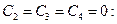

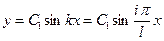. (5.24)

Следовательно, упругая линия при колебаниях весомого вала без дисков представляет собой синусоиду. При колебаниях:

а) 1-го тона 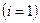- вал не имеет узловой точки (рис.5.8. а);

б) 2-го тона 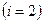- имеется одна узловая точка и на длине вала располагаются две полуволны (рис.5.8. б);

в) 3-го тона 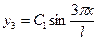- имеются две узловые точки и три полуволны (рис.5.8. в).

В противоположность случаю невесомого вала с одним диском, рассмотренного ранее, для вала постоянного сечения с равномерно распределенной массой получается бесконечно большое число критических скоростей . Отношение критических скоростей вращения при различных колебаниях для рассмотренного вала в соответствии с (5.24) составляет:

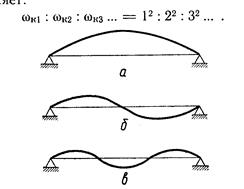
Рис. 5.8 Различные формы колебаний весомого вала без дисков:
а – 1-й тон; б – 2-й тон; в – 3-й тон

Критическая частота вращения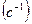

, (5.25)

где 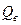- сила тяжести вала, Н; м/с².

Прогиб вала под действием статической нагрузки от собственной массы

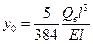. (5.26)

Учитывая (5.25) и (5.26), получим

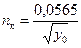. (5.27)