Водородоподобная модель примесного центра
Оценим величину энергии ионизации доноров и акцепторов. Рассмотрим сначала полупроводник, содержащий доноры. Четыре валентных электрона донорного атома участвуют в образовании ковалентной связи с ближайшими соседними атомами. Пятый электрон, не принимая участия в образовании ковалентной связи, взаимодействует с большим числом атомов основного вещества и его связь с донорным атомом уменьшается. Можно провести аналогию между взаимодействием пятого электрона с положительным ионом донора и взаимодействием электрона с ядром в атоме водорода. Однако при решении задачи следует учесть два обстоятельства.
Во-первых, этот электрон находится не только в кулоновском поле положительного иона донора, но и в периодическом поле кристаллической решетки. В связи с этим при описании его движения необходимо использовать вместо обычной массы электрона mn его эффективную массу 
. Во-вторых, между электроном и ионом расположены атомы основного вещества. Будем считать, что взаимодействующие заряды находятся в среде с диэлектрической проницаемостью e.
Запишем уравнение Шредингера для пятого электрона, не участвующего в образовании ковалентной связи
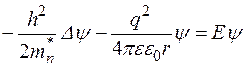. (4.3.1)
Здесь q - элементарный заряд, e0 - электрическая постоянная, e - диэлектрическая проницаемость полупроводника, r - расстояние электрона примеси до ядра "своего" атома.
Значения полной энергии электрона (собственные значения) находят, требуя, чтобы решения уравнения (4.3) удовлетворяли стандартным условиям, то есть были однозначны, конечны, непрерывны. При решении аналогичного уравнения для атома водорода за нулевое значение энергии принимают энергию свободного электрона. В полупроводнике свободные электроны "располагаются" в свободной зоне, поэтому аналогом значения E=0 в атоме водорода будет значение Eс , соответствующее дну зоны проводимости. С учетом сказанного получим выражение для собственных значений энергии электрона донорной примеси
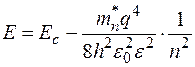, (4.3.2)
где n = 1, 2, 3 ...(целое число).
Эту формулу можно записать следующим образом:
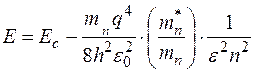, (4.3.3)
или
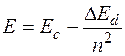, (4.3.4)
где DEd - энергия ионизации донорной примеси.
Из (4.6) следует, что уровень энергии донорной примеси, соответствующий основному состоянию (n=1), находится в запрещенной зоне полупроводника ниже дна зоны проводимости на величину DEd.
Выразим энергию ионизации в электрон-вольтах
эВ (4.3.5)
Энергия ионизации донорной примеси меньше энергии ионизации атома водорода. Оценим её значение для германия. В германии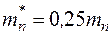 
, диэлектрическая проницаемость германия e =16, подставим эти значения в (4.3.5) и получим величину DEd=0,01 эВ. Это значение достаточно хорошо согласуется с экспериментальными данными.
Для того, чтобы выяснить, насколько правомерно было использование понятия диэлектрической проницаемости, следует оценить число атомов внутри "орбиты" электрона. Расчет радиуса орбиты по водородоподобной модели дает формулу
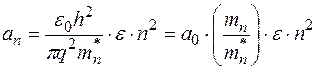. (4.3.6)
Здесь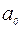 
- радиус первой боровской орбиты в атоме водорода.
Радиус первой орбиты электрона донорной примеси в германии составит величину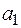 
= 64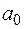 
= 34.10-10 м = 3,4 нм. Если учесть, что постоянная решетки германия равна 0,562 нм, то эта орбита охватывает приблизительно 200-300 узлов решетки. Это подтверждает возможность рассмотрения движения электрона примеси в среде с диэлектрической проницаемостью e .
Рассмотрим теперь полупроводник, содержащий акцепторы.
Трехвалентный атом примеси можно считать системой из взаимодействующих зарядов: положительной дырки и отрицательного иона акцептора. Свободные дырки располагаются в валентной зоне, и минимальная энергия свободной дырки равна EV. Поэтому аналогом E = 0 в атоме водорода будет значение EV. Решение задачи для этого случая дает собственные значения энергии
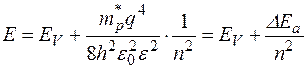, (3 .3.7)
где DEa – энергия ионизации акцепторной примеси. В электрон-вольтах она равна
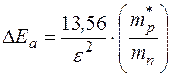эВ. (4.3.8)
Таким образом, уровень акцепторной примеси Ea находится в запрещенной зоне выше потолка валентной зоны на величину DEa= 0,01 эВ.
Итак, мелкие уровни донорной и акцепторной примесей, которые создают атомы элементов V и Ш групп в ковалентных полупроводниках IV группы, достаточно хорошо описываются водородоподобной моделью. Энергия ионизации этих примесей обратно пропорциональна квадрату диэлектрической проницаемости основного полупроводника и пропорциональна эффективной массе носителей заряда.
Элементы других групп (не III и V), введенные в качестве легирующей примеси в полупроводник IV группы, создают глубокие уровни. Описать их с помощью водородоподобной модели не удается.
Дата добавления: 2015-11-10; просмотров: 1327;