Перенесение на местность проектной линии.
Для перенесения на местность проектной линии от исходной точки с помощью мерной ленты или рулетки откладывают в заданном направлении наклонное расстояние, горизонтальное проложение которого равно проектному значению. При этом наклонное расстояние рассчитывают по формуле: D = d + Δ, где D – наклонное расстояние, d – длина проектной линии, Δ – сумма поправок за наклон, за компарирование мерной ленты и за температуру. Поправка за наклон линии вычисляется по формуле: Δdυ = 2D sin2(υ/2), где D = d/cosυ, υ – угол наклона линии. При малых углах наклона линии (меньше 5О) D в формуле для определения поправки можно заменить на d, то есть на длину проектной линии. Кроме этого, поправку за наклон можно рассчитать, зная превышения на концах проектной линии. При этом превышения можно определить по плану или же измерить в натуре. Поправка за наклон должна вводиться в результат измерений с соответствующим знаком плюс или минус. Поправка к длине за компарирование мерного прибора определяется по формуле: Δdk = d/l(lr – l), где l – номинальная длина мерного прибора, lr – фактическая длина мерного прибора. Поправка за температуру вычисляется по формуле: Δdt = αd(t – to), где α - коэффициент температурного расширения материала мерного прибора, t – температура воздуха и почвы во время измерения линии, to - температура, при которой проходил процесс компарирования мерного прибора. Общая поправка при перенесении линии на местность определится как алгебраическая сумма всех трёх поправок, за наклон, за компарирование и за температуру, то есть: Δ = Δdυ + Δdk + Δdt ;
Перенесение на местность проектов зданий и сооружений.По данным геодезической подготовки происходит процесс перенесения проекта здания на местность, который начинается с разбивки на территории строительства так называемых главных и основных осей зданий и сооружений. Главными осями зданий и сооружений называются две взаимно перпендикулярные линии I – I и II –II, относительно которых указываются все остальные данные, необходимые для выноса в натуру всего сооружения или его отдельных частей.
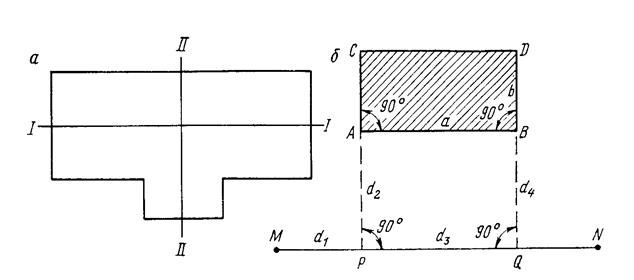
Рис. Главные оси. Схема перенесения оси АВ сооружения на местность.
Основными осями называются линии, определяющие внешний контур здания или сооружения в плане. Главные и основные оси являются геодезической основой для проведения разбивочных работ. Главные оси применяются в процессе разбивки в тех случаях, когда здания или сооружения имеют сложную конфигурацию, или здания связаны между собой технологическими процессами. Для выноса в натуру зданий и сооружений простой геометрической формы разбиваются только основные оси. Главные и основные оси разбиваются на местности от пунктов плановой разбивочной сети. От опорных пунктов государственной геодезической сети разбивается в натуре только одна из осей, от которой в дальнейшем производится разбивка оставшихся деталей проекта. Разбивку осей начинают с выноса двух крайних точек, определяющих положение наиболее длинной продольной оси сооружения. Перенесение в натуру проектных точек осуществляется несколькими способами, а именно: способом прямоугольных координат, способом прямой угловой засечки, способом линейной засечки, способом створной засечки, а также способом полярных координат. Выбор способа определяется в каждом конкретном случае в зависимости от особенностей места предполагаемого строительства, свойств здания или других инженерных, а также экологических или экономических факторов. Рассмотрим способ прямоугольных координат, который применяется в основном для разбивки зданий и сооружений, расположенных вблизи линий государственной геодезической сети или красной линии.
Сущность способа прямоугольных координат заключается в том, что вдоль прямой линии MN откладывают отрезок d1, а затем с помощью теодолита из полученной точки Р восстанавливают перпендикуляр длиной d2. В результате этих построений получают точку А левого угла здания. По аналогии с точкой А получают точку В. При этом ось АВ параллельна линии MN. Для контроля правильности построения измеряют длину линии АВ и определяют ошибку, допущенную при её построении. fd = АВизм – АВпр. Относительная ошибка в длине выносимой линии АВ = а должна находиться в пределах от 1:2000 до 1:10000 в зависимости от вида и назначения разбиваемого здания или сооружения. Для промышленных зданий относительная ошибка должна быть наименьшей. Линия АВ является основной для разбивки всех других осей сооружения. Построением на местности прямых углов в точках А и В и построением проектных линий АС и BD получают на местности проектные точки С и D. Для контроля производят измерения линии CD и диагоналей AD и ВС и сравнивают эти расстояния с их проектными значениями. Разница между численными значениями проектных и измеренных величин не должна выходить за допустимые пределы. В том случае, когда разбивочная ось АВ не параллельна исходной линии MN, положение точки А необходимо определять с помощью решения соответствующих треугольников с использованием известных тригонометрических формул. Необходимые для решения значения горизонтальных углов можно измерить на плане с помощью транспортира. Способ прямоугольных координат также широко используется при перенесении на местность проектов зданий с использованием соответствующей строительной сетки. Допустим, что требуется произвести разбивку осей здания по известным координатам точек их пересечения. В этом случае, например, для построения оси АВ сооружения требуется вычислить длины отрезков ΔxA, ΔyA, ΔxB, ΔyB и отложить длины этих отрезков на местности по соответствующим перпендикулярам. После этого на местности определятся проектные точки А и В. Далее таким же способом получают на местности проектные точки С и D. После чего производят контроль выполненных разбивочных работ.
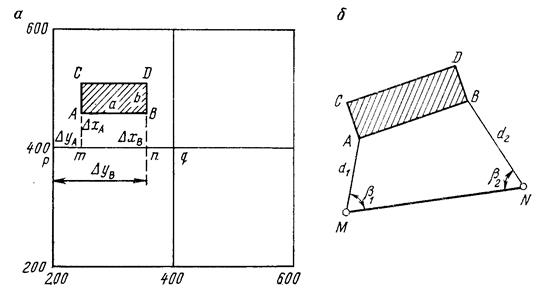
Рис. Схемы перенесения на местность осей сооружений: а - от строительной сетки; б - полярным способом.
Таблица. Вычисление данных для разбивки здания способом прямоугольных координат с использованием строительной сетки
| Вершины | Координаты вершин, м | Расчетные величины | |
| Х | У | ||
| А | ΔXA = ΔXB = 430-400 = 30 ΔYA = 260 – 200 = 60 ΔYB = 340 – 200 = 140 a = 340 – 260 = 80 b = 450 – 430 = 20 | ||
| В | |||
| С | |||
| D |
Способ полярных координат. Данный способ применяется на открытой местности, где удобно производить измерения длины линий и углов. Пусть на местности заданы координаты точек M и N, являющиеся пунктами государственной геодезической сети. Требуется определить на местности положение точек А и В. С этой целью необходимо определить величины дирекционных углов и расстояния между заданными точками геодезической сети и проектными точками. Для расчетов дирекционных углов следует решить обратные задачи геодезии, то есть использовать формулы:
tgαMA = (YA – YM)/(XA – XM); tgαNB = (YB – YN)/(XB – XN);
d1 = (YA – YM)2 + (XA – XM)2; d2 = (YA – YM)2 + (XA – XM)2;
где αMA – дирекционный угол линии МА, αNB – дирекционный угол линии NB, d1 и d2 - соответственно расстояния от точки М до точки А и от точки N до точки В. Далее рассчитывают горизонтальные углы β1 и β2. То есть β1 = αNM – αMA; β2 = αNB – αNM; После произведенных расчетов на местности строят найденные горизонтальные углы и откладывают соответствующие расстояния, получая на местности необходимые точки А и В, которые закрепляют колышками, или другими знаками. Для контроля произведенных работ на местности измеряют полученную линию АВ и находят разность между проектным значением линии и её измеренной величиной. Эта разность, называемая линейной невязкой должна находиться в пределах от 1:2000 до 1:10000. Точки С и D на местности получают построением прямых углов в точках А и В и соответствующих длин линий АС и BD.
При затруднениях в измерениях на местности длины линий для разбивки сооружений в геодезии применяется метод прямой угловой засечки. Сущность способа угловых засечек заключается в построении на местности углов β1 и β2, а также β3 и β4, образованных исходной стороной и направлениями с её конечных точек М и N на определяемые точки А и В. При этом углы засечки не должны быть менее 30О и более 150О.
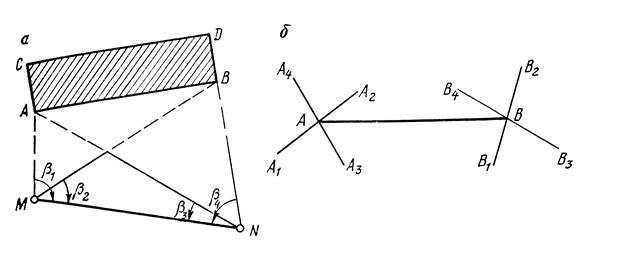
Рис. Схемы перенесения на местность оси сооружения способом угловой засечки
Решая обратные геодезические задачи, описанные подробно в способе полярных координат, находим дирекционные углы α соответствующих направлений. По дирекционным углам направлений α вычисляются величины горизонтальных угловых засечек β:
β1 = αMN – αMA; β2 = αMN – αMВ; β3 = αNA – αNM; β4 = αNB – αNM; Полевые работы по перенесению на местность соответствующих точек способом угловых засечек выполняются в следующем порядке. В точках M и N с помощью теодолита строят последовательно горизонтальные углы β, а в точках начала и конца линии АВ – створы. Точку А1 получают при исходном положении вертикального круга (правое или левое), а точку А2 получают при противоположном положении вертикального круга теодолита, установленного в точке М. Точки А3 и А4 получают аналогично с помощью теодолита, установленного в точке N. Далее в вершины колышков, которые закрепляют на местности точки А1, А2, А3, А4, забивают гвозди и с помощью натянутого шнура на местности получают линии А1 А2 и А3 А4, в точке пересечения которых будет расположена проектная точка А. Аналогично точке А на местности получают точку В. Далее для контроля выполненных работ длину линии АВ измеряют мерной лентой и сравнивают полученное значение с проектной величиной. Величина относительной ошибки измерения должна быть меньше 1:2000. Далее на местности в точках А и В строят прямые углы для получения точек С и D соответствующих противоположных углов проектируемого здания.
Способ линейной засечки применяется в том случае, когда проектные расстояния d1 и d2 не превышают длины мерного прибора, а местность на территории строительства достаточно ровная и открытая.
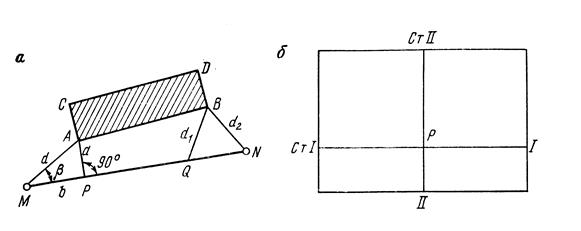
Рис. Схемы перенесения на местность оси сооружения способом линейной засечки и точки Р – способом створов
Координаты точек М и N, а также дирекционный угол линии MN - αMN известны. В этом случае координаты точки А, хА и уА можно рассчитать по формулам: хА = xM + d cos αMA; yА = yM + d sin αMA; где αMA = αMN – β; tg β = a/b; d = a2 + b2; Величины отрезков a и b получают из проектных данных. Координаты точки В вычисляют по формулам: хв = xА + АВ cos αАВ; yв = yА + АВ sin αАВ; где АВ длина линии АВ в проекте здания, αАВ – дирекционный угол линии АВ, измеренный транспортиром. Координаты точки Q на линии MN вычисляются по формулам: хQ = xN + NQ cos αNM; yQ = yN + NQ sin αNM; Далее, зная координаты соответствующих точек, решают обратную геодезическую задачу для определения расстояний d1 и d2. Полевые работы на местности способом линейной засечки выполняются в следующем порядке: в точке Q закрепляют нулевое положение рулетки и радиусом, равным d1 прочерчивают на местности дугу, затем нулевое деление рулетки закрепляют в точке N и прочерчивают дугу радиусом d2. Точка пересечения двух дуг является искомой точкой В.
Точка А на местности строится методом перпендикуляров или полярных координат. После построения на местности точек А и В проводится контрольное измерение линии АВ, определяется относительная ошибка выполненных работ и её допустимость. Затем одним из известных способов на местности определяют положение точек С и D. При выборе параметров линейных засечек желательно, чтобы треугольник QBN был близок к равностороннему.
Перенесение на местность точки способом створной засечки желательно применять при наличии закрепленных на местности главных или основных осей сооружения. При этом способе искомая точка определяется пересечением двух створов, закрепленных на противоположных осях сооружения. Створы можно строить с помощью двух теодолитов или с помощью двух тонких проволок.
Дата добавления: 2015-11-10; просмотров: 2992;
