Основная формула теории упругого режима фильтрации
Пусть в неограниченном горизонтальном пласте постоянной толщины h имеется добывающая скважина нулевого радиуса (точечный сток). Начальное пластовое давление во всем пласте одинаково и равно рк.
В момент времени t = 0 скважина пущена в эксплуатацию с постоянным объемным дебитом Q0. В пласте образуется неустановившийся плоскорадиальный поток упругой жидкости. Распределение давления в пласте (в любой его точке в любой момент времени) р(r, t) определяется интегрированием уравнения (5.27):
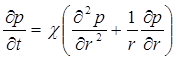, (5.49)
Начальные и граничные условия задачи следующие (см. гл. 2, § 7):
р(r, t) = рк при t = 0,
р(r, t) = рк при r = ∞,
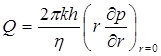= Q 0 = const при r = 0, t > 0. (5.50)
Последнее условие запишем в виде
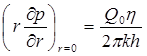. (5.51)
Так же, как в предыдущем случае, проведем анализ размерностей. Искомое распределение давления в пласте зависит от пяти определяющих параметров: r, t,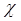 
, pk,, Q 0η/(2πkh), размерности которых следующие:
[r]=L; [t]=T; M=L2 T-1; [pк]=[p],
,
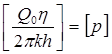где [p],-размерность давления. Тогда давление, приведенное к безразмерному виду, Р = р/рк зависит от двух безразмерных параметров (так как из пяти параметров три имеют независимые размерности (r, t, pк): n = 5, k = 3, n - k = 2.
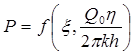
где
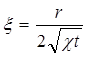
Таким образом задача автомодельна и уравнение (5.49) можно свести к обыкновенному. Продифференцировав (5.52), найдем аналогично предыдущему:
,
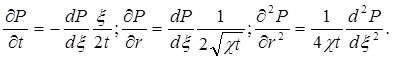Подставив эти выражения в уравнение (5.49), получим обыкновенное дифференциальное уравнение вида
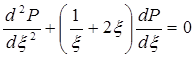, (5.53)
которое нужно проинтегрировать при условиях, полученных из (5.50) Р = 1 при ξ → ∞.
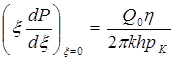. (5.54)
Воспользуемся подстановкой
,
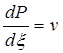тогда вместо уравнения (5.53) будем иметь
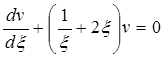
или
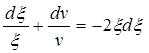. (5.55)
Проинтегрировав (5.55), получим:
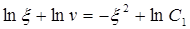, (5.56)
где C1-постоянная интегрирования.
Потенцируя (5.56), получим:
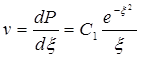, (5.57)
Проинтегрировав (5.57), и учтя первое из условий (5.54), получим:
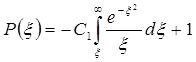, (5.58)
Умножая равенство (5.57) на ξ устремляя ξ → 0 и используя второе условие (5.54), найдем, что
.
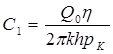Тогда из (5.58) получим:
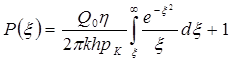. (5.59)
Интеграл в последней формуле легко свести к табличному следующий подстановкой:
,
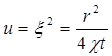тогда
.
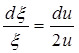Перейдя также от безразмерного давления Р к размерному р = Ррк получим:
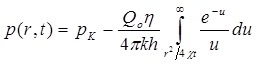. (5.60)
Интеграл в формуле (5.60) называется интегральной показательной функцией, которая табулирована и обозначается
.
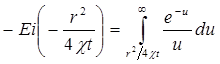Следовательно, давление в любой точке плоскорадиального потока в условиях упругого режима фильтрации определяется по формуле
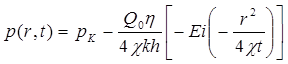. (5.61)
Формула (5.61) получила название основной формулы теории упругого режима фильтрации. Она имеет широкое практическое применение и, в частности, используется при интерпретации результатов исследования скважин, в расчетах распределения давления при фильтрации упругой жидкости и т.д.
Интегральную показательную функцию можно представить в виде ряда
,
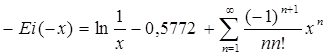который сходится при всех значениях х 0 < х < ∞. При изменении аргумента х от 0 до ∞ функция - Ei(-х) быстро убывает от ∞ до 0. График этой функции приведен на рис. 5.3. При малых значениях х суммой ряда можно пренебречь, тогда
.
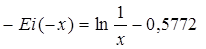При этом погрешность не превосходит:
 |
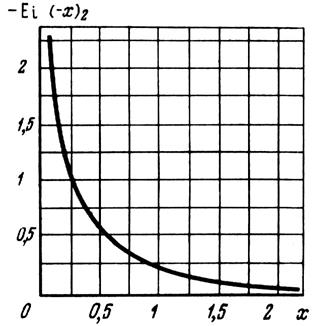Рис. 5.3. График интегральной показательной функции
0,25% если х =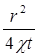 
≤ 0,01;
1% если х ≤0,03;
5,7% если х≤0,1;
9,7% если х ≤0,14.
Следовательно, для значений 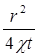≤ 1 давление можно определять по формуле
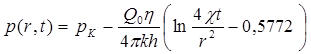. (5.62)
Из (5.61) находим, что расход жидкости через любую цилиндрическую поверхность радиусом r и скорость фильтрации определяются соответственно по формулам
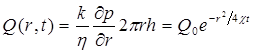, (5.63)
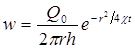. (5.64)
Из последней формулы следует, что стационарная скорость wстац =
=Q0/(2πrh) достигается очень быстро на небольших расстояниях от скважины, так как значение коэффициента пьезопроводности обычно велико.
При теоретическом исследовании неустановившихся процессов перераспределения пластового давления удобно пользоваться безразмерными параметрами Фурье fo и Fo, играющими роль безразмерного времени и определяемыми по следующим равенствам:
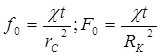, (5.65)
 |
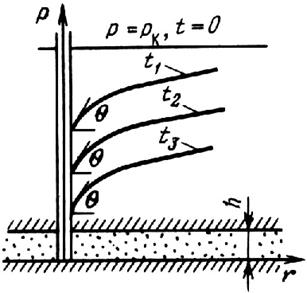Рис. 5.4. Пьезометрические кривые при пуске скважины с постоянным дебитом Q0
где rc - радиус скважины; Rк, - радиус кругового контура питания или радиус круговой непроницаемой границы пласта.
В зависимости от специфики решаемой задачи удобно пользоваться тем или другим из указанных параметров Фурье.
Строго говоря, основная формула теории упругого режима (5.61) справедлива лишь для случая точечного стока (при rc = 0) в неограниченном пласте (Rк = ∞).
Для оценки влияния конечного радиуса возмущающей скважины rc на результаты расчетов давления В. Н. Щелкачев сравнил результаты расчетов давления по формуле (5.61) с точной формулой Ван-Эвердингена и Херста (см. § 8), учитывающей конечный радиус скважины rc. При этом В. Н. Щелкачев установил, что погрешность подсчетов давления по формуле (5.61) составляет:
0,6% при fo = 100;
2,3% при fo = 25;
5% при fo = 10;
9,4% при fo = 5.
Оценим практическое значение этой погрешности. Допустим, что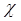 
= 1 м2/с, rc = 0,1 м; тогда полагая fo = 100, найдем:
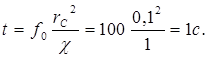
Следовательно, уже через 1 с после пуска скважины расчеты забойного давления, выполненные по формуле (5.61), будут иметь погрешность, не превышающую 0,6%. Отсюда следует, что для скважин обычных размеров формула (5.61) обеспечивает высокую степень точности уже на самой ранней (а тем более на поздней) стадии процесса перераспределения давления.
Непосредственными расчетами В. Н. Щелкачевым было установлено, что в громадном большинстве практически интересных случаев изменение давления при работе скважины в конечном открытом пласте можно в течение достаточно длительного времени изучать при помощи простой формулы (5.61) для бесконечного пласта. При этом погрешность в подсчетах забойного давления не превзойдет:
0,08% при Fo ≤ 0,2:
1 % при Fo ≤ 0,35;
1,9% при Fo ≤ 0,5.
Для расчетов пластового давления в любой точке открытого кругового пласта в случае r ≤ 0,1 Rк можно с высокой степенью точности (до 0,2%) пользоваться формулой (5.61) для бесконечного пласта, если при этом Rк ≥105 rс , Fo ≤ 0,2.
В дополнение к указанным оценкам можно еще отметить, что различие в величинах забойных давлений в условиях конечного (открытого и закрытого) и бесконечного пластов не превзойдет 1%, если Fo ≤ 0,33, Rк ≥ 50 rс, или если Fo ≤ 0,35, Rк ≥ 1000 rс.
Решение дифференциального уравнения Фурье (5.49) для различных случаев фильтрации упругой жидкости в ограниченных открытых и закрытых пластах представляются бесконечными рядами по функциям Бесселя (см. § 8).
В заключение покажем, как ведут себя пьезометрические кривые вблизи скважины, которая эксплуатируется с постоянным дебитом Q0 (рис. 5.4). Для точек вблизи забоя можно пользоваться формулой (5,62); продифференцировав ее по координате r, найдем градиент давления:
.
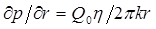Из этой формулы следует, что градиент давления для значений r, удовлетворяющих неравенству r2 ≤ 0,03 • 4 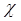t, практически не зависит от времени и определяется по той же формуле, что для установившейся плоскорадиальной фильтрации несжимаемой жидкости. Для указанных значений r пьезометрические кривые представляют собой логарифмические линии (см. рис. 5.4). Давление на забое скважины падает с течением времени, углы наклона касательных θ на забое одинаковы для всех кривых.
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ТЕОРИИ УПРУГОГО РЕЖИМА
Решения различных краевых задач неустановившейся фильтрации упругой жидкости в упругой пористой среде в условиях как бесконечного, так и конечного пластов можно получить при помощи хорошо известных методов интегрирования линейного дифференциального уравнения в частных производных-уравнения теплопроводности (5.14).
Однако во многих случаях эти решения представляются громоздкими формулами в виде бесконечного медленно сходящегося ряда или несобственного интеграла, содержащего специальные функции.
В связи с этим были предприняты поиски приближенных эффективных решений задач неустановившейся фильтрации.
Рассмотрим здесь некоторые из разработанных приближенных методов, получивших широкое применение при решении задач теории упругого режима.
Дата добавления: 2015-11-10; просмотров: 6834;