Информатика. В последнее время получили большое распространение системы поддержки принятия решений, помогающие человеку в задачах выбора.

ТЕОРИЯ

ПРИНЯТИЯ РЕШЕНИЙ

Термин «принятие решений» встречается во многих научных дисциплинах.

Экономика. Экономика характеризует отношение между производителем и потребителем. Считается, что у людей есть «внутренние весы», на которых «взвешивается» полезность, то есть привлекательность различных товаров. Поэтому она определяет правила рационального поведения людей в задачах выбора.

Психология. Термин «принятие решений» широко используется в когнитивной психологии. Психологи изучают, как влияют особенности человеческой системы на переработку информации, на выбор тех или иных решений. Особенно популярным стало это направление в последние годы в связи с развитием рыночных отношений.

Политология. Одним из основных объектов изучения в политологии является механизм принятия лидерами политических решений.

Математика. Тесно связано с принятием решений такое научное направление как исследование операций. Исследуются задачи обоснования свойств функции полезности в зависимости от ограничений, накладываемых на правила выбора.

Информатика. В последнее время получили большое распространение системы поддержки принятия решений, помогающие человеку в задачах выбора.

Таким образом, принятие решений — это прикладная научная дисциплина. Основным в ней является сам процесс выбора человеком одного из вариантов решений. Эта наука изучает, как человек принимает решения и как следует ему в этом помогать, создавая специальные методы и компьютерные системы.

В жизни решения часто принимают интуитивно, исходя из жизненного опыта. Но бывает, что интуиция подводит человека. Например, рассмотрим числовой ряд

.

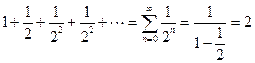Это геометрическая прогрессия со знаменателем q = ½. Сумма этого ряда равна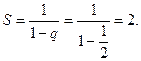

На предыдущий похож следующий числовой ряд, который называется гармоническим

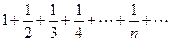
Спрашивается, стремится ли он к конечному пределу или является расходящимся. Подсчитаем суммы первых 10 членов ряда, приведённых в следующей таблице.

Таблица – Частичные суммы ряда
Частичные суммы	Значения
	1.0000
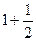
	1.500
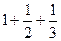
	1.833
	2.083
	2.233
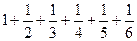
	2.250
	2.642
	2.767
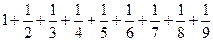
	2.879
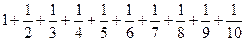
	2.979

Мы видим, что элементы суммы вносят всё меньший вклад в общий результат, и общая сумма ряда возрастает очень медленно. Интуитивно может показаться маловероятным, что ряд может расходиться. Однако сгруппируем члены ряда следующим образом:

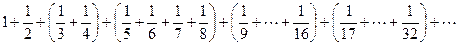
Суммы слагаемых во всех скобках будут больше ½. Действительно, возьмем последний член четвёртой группы, равный 1/8, и заменим на него предшествующие члены: 1/5, 1/6 и 1/7. Сумма в скобках станет равной ½. Следовательно, исходная сумма в скобках больше ½, а сумма членов ряда в двух подряд стоящих скобках больше 1. Чем больше групп, тем больше сумма, и ряд расходится.

Предположим, что имеется ряд событий, которые влияют друг на друга всё в меньшей степени, как в вышеприведённой последовательности. Естественно предположить, что это влияние, в конечном счете, уменьшится. Однако этот результат может быть ошибочным, если сопоставленные этим влияниям числа возрастают в группах гармонического ряда.