Линейный двухсвязный список

Односвязный список обеспечивает возможность продвижения лишь в одном направлении - от начала к концу - при просмотре списка. Линейный двусвязный список (linear double-linked list) дает возможность двигаться в одном из двух направлений. Он отличается от односвязного тем, что каждый его элемент содержит два логических указателя, один из которых, прямойуказатель(direct pointer), адресует, как и в односвязном списке, следующий справа элемент, а другой,обратный указатель(backward роinter), адресует предыдущий элемент списка. Логическая структура линейного двусвязного списка (ЛДС) представлена на рисунке 6.7. Начало и конец такого списка логически эквивалентны, так как доступ к любому элементу может быть осуществлен с любого конца. Поэтому вместо терминов «начало» и «конец» списка используются термины «левый конец» и «правый конец».

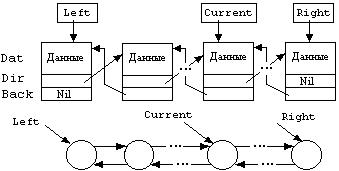
Рисунок 6.7 - Два варианта изображения логической структуры
линейного двухсвязного списка

В кольцевом двухсвязном списке прямой указатель самого правого узла ссылается на самый левый элемент, и обратный указатель самого левого узла адресует самый правый в логической структуре узел. Логическая структура кольцевого двухсвязного списка представлена на рисунке 6.8

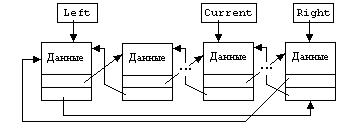
Рисунок 6.8 - Кольцевой двухсвязный список

6.3.1 Структура элемента двухсвязного списка

Структура узла двухсвязного списка, в общем случае, и, в частности, линейного двухсвязного списка, может задаваться следующими описаниями:

Type

PNodeDList = ^TNodeDList;

TNodeDList = Record

Key: Integer;

Dat: <идентификатор типа данных>;

Dir, Back: PNodeDlist;

End;

Тип TNodeDList - это самоадресующийся тип. Он предусматривает наличие в элементе двухсвязного списка двух структурных указателей: поле Dir предназначено для размещения указателя на следующий правый элемент, поле Back - на следующий элемент, расположенный в логической структуре слева. Поле Key введено с целью облегчения дальнейших пояснений.

Для иллюстрации операций в ЛДС нам потребуется описание некоторых переменных-курсоров:

Var Left, Right, Current, G: PNodeDList;

6.3.2 Реализация операций в линейном двухсвязном списке

Пока список пуст, курсоры его концов Left и Right не должны никуда указывать. Следовательно, способ инициализировать двухсвязный список заключается в присваивании этим указателям значения Nil:

Left:= Nil; Right:= Nil;

Текст программного кода формирования линейного двухсвязного списка из N элементов может быть записан следующим образом:

Var i: Integer;

Begin

i:= N;

While i > 0 Do Begin

New(Current);

Current^.Dir := Left; Current^.Back:= Nil;

IF i = N Then Right:= Current

ElseCurrent^.Dir^.Back:= Current;

Left:= Current; Current^.Key:= i;

<заполнение полей Current^.Dat>

i:= i-1;

End; {While}

End;

Под управлением этого кода список дополняется элементами в направлении справа налево, т. е. первый созданный элемент окажется концевым правым элементом, а последний расположится на левом конце. Курсор текущего элемента будет ссылаться на левый концевой элемент.

Программа просмотра ЛДС аналогична программе просмотра односвязного списка. Необходимо только указать от какого конца, левого или правого, следует начинать продвижение по узлам. Например, если требуется выполнить просмотр списка слева направо, то можно использовать следующий фрагмент:

Current:= Left;

While Current <> Nil Do Begin

With Current^ Do Begin

<действия с полями элемента Current^>

End;

Current:= Current^.Dir;

End;

Для прохождения узлов справа налево в приведенном фрагменте нужно заменить идентификаторы Left на Right и Dir на Back.

Рассмотрим наиболее общий случай вставки, когда элемент, рядом с которым в логической структуре вставляется новый элемент, не является кольцевым элементом. Коды, реализующие дополнение линейного двухсвязного списка со стороны одного из концевых узлов, во многом напоминают вставку в начало односвязного списка. Итак, фрагмент программы вставки справа от текущего элемента, расположенного в средней части ЛДС, может содержать следующую последовательность операторов:

New(G); G^.Key:= 20;

G^.Dir:= Current^.Dir;

Current^.Dir:= G;

G^.Back:= Current;

G^.Dir^.Back:= G;

На рисунке 6.9 а показана логическая схема, изображающая ЛДС из трех элементов и элемент G^, созданный в результате выполнения первой строки рассматриваемого фрагмента. А на рисунке 6.9 б показана логическая структура, сформированная в после завершения вставки.

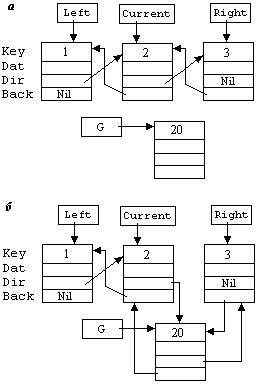
Рисунок 6.9 - Операция вставки в ЛДС

Для иллюстрации операции удаления приведем фрагмент кода, при выполнении которого удаляется текущий элемент с перемещением его указателя на один элемент направо. Этот фрагмент может иметь вид:

G:= Current;

Current:= Current^.Dir;

G^.Back^.Dir:= Current;

Current^.Back:= G^.Back;

Dispose(G);

Плексы

6.4.1 Нелинейный двухсвязный список

Односвязный список всегда линейный. Двусвязный же список может быть и нелинейным, о чем свидетельствует следующий пример.

Представим себе, что двухсвязный список формируется из данных об абитуриентах ВУЗа. Причем первый указатель связывает элементы списка в порядке подачи абитуриентами документов в приемную комиссию, а второй – устанавливает упорядоченность элементов, соответствующую алфавитному порядку фамилий абитуриентов. Тогда, если к текущему моменту времени заявления о поступлении в ВУЗ подали шестеро абитуриентов, двусвязная структура, состоящая из данных об абитуриентах, может принять вид, изображенный на рисунке 6.10.

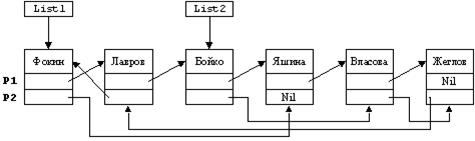
Рисунок 6.10 - Логическая структура нелинейного двухсвязного списка

Ссылки List1 и List2 являются указателями двух отдельных односвязных списков, в каждый из которых одновременно входят все шесть элементов. Поля Р1 и Р2 всех элементов служат для хранения структурных ссылок, с помощью которых элементы связываются, формируя тем самым каждый из двух списков.

На рисунке 6.10 показано лишь одно из содержательных полей узлов, а именно, поле фамилии абитуриента (объекта предметной области). Из рисунка видно, что в списке, сформированном с помощью ссылки Р1, установлен следующий порядок следования узлов:

Фокин ® Лавров ® Бойко ® Яшина ® Власова ® Жеглов

В цепном списке, указателем которого является List2, - этот список сформирован с помощью структурной ссылки Р2 - элементы располагаются в следующем порядке:

Бойко ® Власова ® Жеглов ® Лавров ® Фокин ® Яшина

Представление логической структуры этого же двухсвязного списка может быть преобразовано к другому, эквивалентному, виду, который показан на рисунке 6.11. Рисунки 6.10 и 6.11 отображают структуру одного и того же нелинейного двухсвязного списка. Сопоставление рисунков 6.10 и 6.11 показывает, что оба цепных списка двухсвязной структуры, рассматриваемые по отдельности, являются линейными. Вся структура в целом, с учетом обеих связок, - не линейна

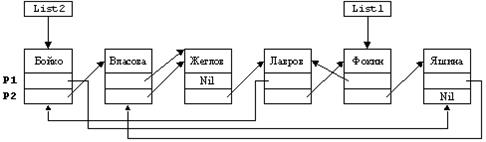
Рисунок 6.11 - Эквивалентная логическая структура нелинейного
двухсвязного списка, изображенного на рисунке 6.10

6.4.2 Нелинейный трехсвязный список

Несложно представить трехсвязный список, содержащий информацию об абитуриентах, в котором две структурных ссылки объединяют узлы так же, как на рисунках 6.10 и 6.11, а третья ссылка Р3 связывает те элементы (в алфавитном порядке), которые относятся к абитуриентам, обладающим правами преимущественного поступления в ВУЗ. Логическая структура такого списка показана на рисунке 6.12. На этом рисунке штриховыми линиями показаны структурные ссылки, объединяющие элементы с помощью поля Р3. Назовем этот цепной список Р3-списком.

В цепном списке, организованном с помощью структурного указателя Р3, очевидно, будет содержать не все элементы. В нашем примере (см. рисунок 6.12) в Р3-списке содержится три элемента, которые упорядочены ссылкой Р3 следующим образом:

Бойко ® Фокин ® Яшина

Указателем Р3-списка является внешний указатель List3. Этот пример показывает, что необязательно, чтобы каждый элемент общей списковой структуры непременно входил во все цепные списки одновременно.

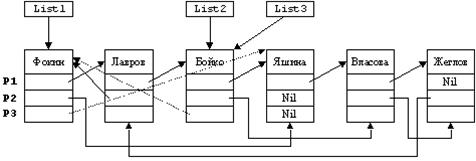
Рисунок 6.12 - Логическая структура нелинейного трехсвязного списка

6.4.3 Определение плекса и его общие признаки

В общем случае возможно создание многосвязного списка, каждый элемент которого может содержать К полей (К = 2, 3, 4 …) структурных указателей. Как показывают логические структуры нелинейных связных списков, изображенные на рисунках 6.10 - 6.12, многосвязный список как бы «прошит» в разных направлениях многими указателями. Поэтому такие списки называют прошитыми списками или плексами (plexus - сплетение, переплетение).

Сформулируем общие признаки плексов:

1) все элементы такой структуры содержат одинаковое количество полей структурных указателей, число которых К- степень связности - является важной характеристикой структуры;

2) не обязательно, чтобы каждый элемент общей структуры входил во все К цепных списков одновременно;

3) каждый отдельный список, организованный с помощью одной и той же ссылки, поле для которой имеется во всех элементах, является односвязным цепным, а значит и линейным списком, если не принимать во внимание другие связи;

4) на каждый элемент может ссылаться произвольное число других элементов структуры, и от любого элемента к другим элементам может быть направлено произвольное число указателей, но в обоих случаях число таких указателей-ссылок не превышает К;

5) вся структура в целом не линейна, поскольку, если учитывать все связки, для каждого элемента не может быть определен единственный элемент-предшественник и единственный элемент-последователь.