Оптимум обеспечения коллективного блага для малой группы (Модель М. Олсона)

Малые группы во многих случаях оказываются гораздо более эффективными и жизнеспособными, чем большие группы.

Индивиды создают какую-либо малую группу (организацию) также для достижения возможности получать коллективное благо.

Если существует такое количество коллективного блага, которое можно получить при достаточно низких издержках, и что некий индивид в соответствующей группе выиграет от приобретения его полностью за свой счет, тогда существует вероятность, что такое благо будет произведено (получено).

В этом случае общая выгода будет настолько велика по сравнению с общими издержками, что доля прибыли одного индивида превысит общие издержки.

Нашей целью является определить:

1) оптимальное для каждого индивида количество блага;

2) будет ли при этом оптимуме производиться коллективное благо.

Введем следующие переменные:

C – издержки по достижению единицы коллективного блага;

T - объём коллективного блага;

S_g – размер группы – const;

F_i – часть общей выгоды, которая досталась индивиду – const;

V_g = (S_gT) – выгода группы (ценность блага для группы);

V_i – ценность блага для индивида (выгода индивида).

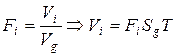, или ;

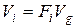A_i – преимущества, которые получит индивид в результате получения какого-то количества коллективного блага;

;

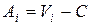A_i будет изменяться в зависимости от T => .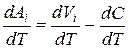

Условием первого порядка для максимизации выгоды индивида будет .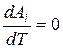

Условием второго порядка – .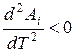

Так как ,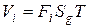

а F_i и S_g – признаются постоянными (в противном случае оптимум недостижим), то 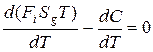, следовательно

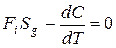
Таким образом, мы найдем, какое количество коллективного блага купил бы индивид, действуя самостоятельно, если бы он хотел купить его сколько-нибудь.

Можно придать этому результату общий смысл. Поскольку оптимальный вариант может быть найден, когда выполняется:

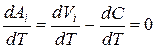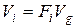если , то

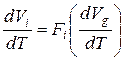, следовательно,

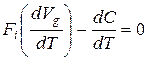
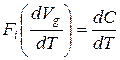
Это означает, что оптимальное количество группового блага, предназначенного для индивида, можно достичь, когда изменение выгоды всей группы, помноженное на долю индивида, равняется изменению общих издержек группы по достижению этого блага.

Другими словами, увеличение дохода группы 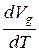должно превышать увеличение издержек на столько же, насколько доход группы превышает доход индивида, т.е. на .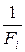

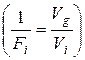В теории групп важен вопрос не сколько будет произведено коллективного блага, а будет ли оно обеспечено вообще.

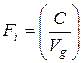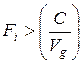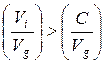Оптимум индивидуума, действующего самостоятельно, будет при так как, если , то , следовательно, 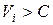, поэтому если 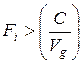, то выгода индивида от коллективного блага превышает издержки.

Это означает, что коллективное благо будет обеспечено, если издержки по добыче коллективного блага настолько малы по сравнению с выгодой для группы, что общая выгода превышает общие издержки настолько же, насколько она превышает выгоду отдельного индивида.

На основании вышесказанного можно сформулировать правило:

Коллективное благо будет обеспечено, если превышение общей выгоды при покупке (производстве) коллективного блага над общими издержками в 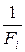раз (так как 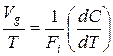), сопровождается условием, что общая выгода превышает общие издержки в большее число раз, чем общая выгода группы превышает выгоду индивида, т.е. .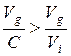

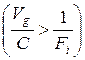Чтобы определить, реально ли предположение, что группа добровольно возьмет на себя производство коллективного блага, необходимо выполнение двух условий:

1) оптимальное для каждого индивида количество коллективного блага, определяется равенством:

;

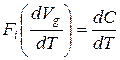2) если при покупке определенного количества коллективного блага выгода группы превосходит общие издержки в большей мере, чем она превосходит выгоду одного индивида, тогда существует основание полагать, что коллективное благо будет обеспечено и выгода индивида превысит общие издержки, связанные с добыванием коллективного блага, т.е. благо может производиться и в случае .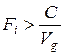

Это можно проиллюстрировать с помощью графика:

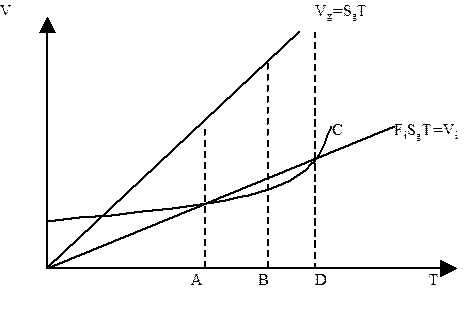
Рис.Оптимум производства коллективного блага для группы