Измерение информации
Кроме качественных, информация имеет количественные характеристики. При этом используются разные подходы к измерению количества информации. Некоторые подходы дают объективные оценки количества информации, другие – дают субъективные оценки. Эти оценки носят название «меры».
К объективным (независящим от субъекта, получающего информацию) относится синтаксическая мера. В синтаксической мере определяется объем данных (Vд) и количество информации (Ic). Эта мера оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту. На синтаксическом уровне учитываются тип носителя и способ представления информации, скорость передачи и обработки, размеры кодов представления информации.
Объем данных указывает количество места, занимаемое информацией на машинном носителе. Так как информация в дискретном виде хранится в виде записей на некотором языке с определенным алфавитом, можно считать, что объем информации – это количество символов, составляющих запись, умноженное на размер места, занимаемый одним символом.
Для автоматизации работы с данными, относящимися к различным типам, важно унифицировать их форму представления. Для этого используется кодирование.
Кодирование - представление данных одного типа через данные другого типа.
Своя система существует и в вычислительной технике – это двоичное кодирование, которое основано на представлении данных последовательностью всего двух знаков: 0 и 1. Эти знаки называются двоичными цифрами (по-английски ‑ binary digit или сокращенно ‑ bit).
Одним битом могут быть выражены два понятия (да, или нет, истина или ложь). Если количество битов увеличить до двух, то уже можно выразить четыре различных понятия (комбинациями 00 01 10 11). Тремя битами можно закодировать восемь различных значений (000 001 010 011 100 101 110 111). Увеличивая на единицу количество разрядов двоичного кодирования, мы увеличиваем в два раза количество значений, которое может быть выражено в данной системе.
С помощью двоичного кода можно кодировать и текстовую информацию, сопоставляя каждому символу алфавита определенное целое число. Восьми двоичных разрядов достаточно для кодирования 256 символов.
В настоящее время для кодирования одного символа текстовой информации используется байт – это минимальная единица объема информации. В принципе, байт определяется для конкретного компьютера как минимальный шаг адресации памяти, который на старых машинах не обязательно был равен 8 битам (а память не обязательно состоит из битов, например, троичный компьютер). В современной традиции, байт часто считают равным восьми битам. 1 байт = 8 бит.
Примерами алфавитов являются: таблица символов ASCII, в количестве 256 кодов; набор цветовой гаммы TRUECOLOR, содержащий свыше 16 миллионов цветов. В цифровой двоичной вычислительной машине в первом случае для хранения одного элемента алфавита требуется 8 двоичных разрядов, во втором – 24 разряда.
Для измерения информации также используются производные единицы:
Таблица 1. Единицы измерения объема данных
| Название | Обозначение | Степень |
| байт | байт | 20 |
| килобайт | Кбайт | 210 |
| мегабайт | Мбайт | 220 |
| гигабайт | Гбайт | 230 |
| терабайт | Тбайт | 240 |
| петабайт | Пбайт | 250 |
| эксабайт | Эбайт | 260 |
| зеттабайт | Збайт | 270 |
| йоттабайт | Йбайт | 280 |
Особое название имеет 4 бита — ниббл (полубайт, тетрада, четыре двоичных разряда), которые вмещают в себя количество информации, содержащейся в одной шестнадцатеричной цифре.
210 - называется «двоичной тысячей» = 1024.
В килобайтах измеряют сравнительно небольшие объемы данных. Условно можно считать, что одна страница неформатированного машинописного текста составляет около 2 Кб.
Лекция 2
Количество информации выступает другой величиной в синтаксической мере. Этот параметр определяется уменьшением неопределенности (незнания) об объекте или явлении при появлении новой информации. Количество информации, уменьшающее неопределенность в 2 раза носит название 1 бит. Если еще раз уменьшить неопределенность в 2 раза (всего – в 4 раза), количество информации увеличится еще на 1 бит. Таким образом, количество информации – есть величина логарифмическая. Это означает, что когда несколько событий или объектов рассматриваются как один, количество возможных состояний перемножается, а количество информации — складывается.
Иными словами, количество информации можно представлять как логарифм количества состояний. Количество состояний – число целое. Наименьшее целое число, логарифм которого положителен — 2. Соответствующая ему единица — бит — является основой исчисления информации в цифровой технике.
Количество информации, полученное в результате какого-либо события, зависит от того, сколько вариантов этого события могло быть, точнее с какой вероятностью событие могло произойти с данным конкретным результатом. В 1948 г. Шеннон предложил формулу расчета количества информации Ic при возникновении события, вероятность которого равна pc :
Ic = - log2(pc)
Например, при бросании монеты вероятность выпадения «орла» (как и «решки») равна ½. Тогда количество информации при выпадении орла вычисляется:
Iорел = - log2(1/2) = log2(2) = 1 (бит)
Такой подход к измерению информации называется вероятностным. Количество информации зависит от вероятности события. Например, сообщение, что летом выпал снег, несет больше информации, чем сообщение что шел дождь так как первое событие гораздо менее вероятно.
Полное количество информации о системе, которая может иметь N различных состояний (т.е. в которой может произойти N событий), каждое из которых имеет вероятность pi, на синтаксическом уровне определяется по формуле Шеннона:

Если вероятности всех событий равны между собой, т.е. pi=1/N, то полное количество информации о системе будет максимальным, и составит:
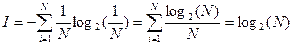
В качестве примера, рассмотрим задачу вытаскивания шара из мешка, в котором лежит 15 белых шаров и один черный. Сообщение, что в первой попытке вытащен черный шар несет количество информации:
Iч = - log2(1/16)= log2(16) = 4 бит,
а сообщение, что вытащен белый шар -
Iб = - log2(15/16)= log2(16/15) = 0.0645 бит
Отсюда видно, что количество информации может быть меньше 1.
Другой пример: Пусть у некоторого студента вероятность получить на экзамене «5» составляет 25%, «4» - 50%, «3» - 12.5% и «неуд» - 12.5%. Тогда количество информации о полученной оценке (полное количество информации) равно:
 ,
,
тогда, как количество информации, что студент получил 5 баллов равна:
I5 = - log2(1/4) = 2 бит.
Часто информация кодируется числовыми кодами в той или иной системе счисления, особенно это актуально при представлении информации в компьютере. Допустим, что по каналу связи передается n-разрядное сообщение, использующее m различных символов. Так как количество всевозможных кодовых комбинаций будет N=mn, то при равной вероятности появления любой из них количество информации, приобретенной абонентом в результате получения сообщения, будет
I=log N=n.log m — формула Хартли.
Если в качестве основания логарифма принять m, то I = n. В данном случае количество информации (при условии полного априорного незнания абонентом содержания сообщения) будет равно объему данных I=VД, полученных по каналу связи.
Количество информации – это наиболее важная и универсальная характеристика информации. Хотя объем и количество информации иногда измеряют с помощью одних и тех же единиц, их нельзя путать и смешивать между собой.
Например, сообщение «на выборах президента США из демократов и республиканцев победил представитель демократической партии» состоит из 101 символа (это объем информации), но содержит всего 1 бит (это количество информации), так как в 2 раза уменьшает неопределенность – кто из двоих победил.
Коэффициент (степень) информативности (лаконичность) сообщения определяется отношением количества информации к объему данных, т.е.
Y = Ic/Vд
С увеличением Y уменьшаются объемы работы по преобразованию информации (данных) в системе. Поэтому стремятся к повышению информативности, для чего разрабатываются специальные методы оптимального кодирования информации
В семантической мере анализируется смысловое содержание информации.
Для измерения смыслового содержания информации, т.е. ее количества на семантическом уровне, наибольшее признание получила тезаурусная мера, которая связывает семантические свойства информации со способностью пользователя принимать поступившее сообщение. Для этого используется понятие тезаурус пользователя.
Тезаурус — это совокупность сведений, которыми располагает пользователь или система.
В зависимости от соотношений между смысловым содержанием информации S и тезаурусом пользователя Sp изменяется количество семантической информации Ic, воспринимаемой пользователем. Рассмотрим два предельных случая, когда количество семантической информации Ic равно 0:
• при Sp→0 пользователь не воспринимает, не понимает поступающую информацию;
• при Sp→: пользователь все знает, и поступающая информация ему не нужна.
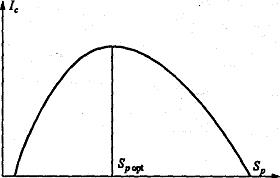
Рисунок 1. Зависимость количества семантической информации, воспринимаемой потребителем, от его тезауруса.
Максимальное количество семантической информации Ic потребитель приобретает при согласовании ее смыслового содержания S со своим тезаурусом Sp (Sp = Sp opt), когда поступающая информация понятна пользователю и несет ему ранее не известные (отсутствующие в его тезаурусе) сведения. Относительной мерой количества семантической информации может служить коэффициент содержательности C, который определяется как отношение количества семантической информации к ее объему:
C=Ic/Vд
Прагматическая мера определяет практическую полезность информации.
Эта мера определяет полезность информации (ценность) для достижения пользователем поставленной цепи. Эта мера - также величина относительная, обусловленная особенностями использования этой информации в той или иной системе.
Ценность информации целесообразно измерять в тех же самых единицах (или близких к ним), в которых измеряется целевая функция.
Часто, в качестве прагматической меры используют денежные единицы, например: «Ваша информация стоит 10 000 $», или «эта информация и ломаного гроша не стоит».
Лекция 3
Дата добавления: 2015-08-08; просмотров: 1700;
