Движение электронов в ускоряющем электрическом поле

Рассмотрим однородное электрическое поле с напря­женностью Е = U/d (рис. 1.1).

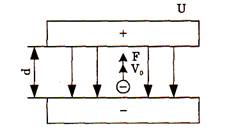
Рис. 1.1. Однородное электрическое поле

На единичный заряд, помещенный в электрическое поле, действует сила F, равная по величине напряженности этого поля Е, т. е. F = Е. Заряд электро­на по модулю равен е = 1,6 • 10^-19 Кл. Действующую на электрон е силу можно вычислить по формуле

F = - еЕ.

Знак «-» показывает, что сила F, действующая на электрон, направлена против линии напряженности электрического поля Е. Под действием данной силы электрон будет двигаться равноускоренно и приобретет максимальную скорость в конце пути. Ускоряющим электрическим полем называют такое поле, у которого линии напряженности направлены навстречу вектору начальной скорости электрона V₀. Работа А по перемеще­нию электрона из одной точки поля в другую равняется произведению заряда электрона на разность потенциалов U между этими точками,

А = Fd = еЕd = eUd/d = е U.

Данная работа затрачивается на сообщение электрону кинетической энергии W_к,

W_к = m (V – V₀)²/2

где V - скорость электрона в конечной точке перемещения;

V₀ - скорость электрона в точке начала движения;

m - масса электрона, со­стоянии покоя, равная 91 • 10^-29 г.

Если электрон находится в электрическом поле в со­стоянии покоя, такое поле называют электростатическим. Предположим, что начальная скорость электрона равна 0, то есть V₀ = 0.

Работа по перемещению электрона равна кинетичес­кой энергии электрона,

А = W_к.

Вместо обозначения работы А равное ей произведение еU. Учитывая, что мы приняли равной 0 начальную скорость электрона, можем упростить формулу нахождения кинетической энергии, записав W_к = mV²/2. Теперь можно записать равенс­тво работы по перемещению заряда и его кинетической энергии в следующем виде,

eU = mV²/2.

Cкоростm электрона в конечной точке.

Так как заряд электрона е и его масса m являются константами, то

V = 600√U.

Из данной формулы видно, что скорость электрона в электрическом поле определяется только величиной напряжения между двумя точками поля.