Демодулятор с ЧМ-АМ-АД

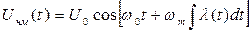- ЧМ колебание (4.1)

Реализация:

Рис.4.2детектор(ЧМ-АМ-АД)

Продифференцируем (4.1)

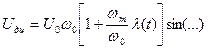(4.2)

На выходе АД:

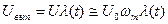(4.3)

В качестве дифференциатора – любая линейная цепь имеющая наклон АЧХ

К_дц(ω) = ωτ - передаточная функция идеального дифференциатора

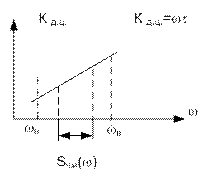
Рис.4.3АЧХ идеального дифференциатора

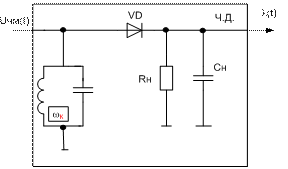
Рис.4.4пример реализации частотного детектора

АЧХ колебательного контура

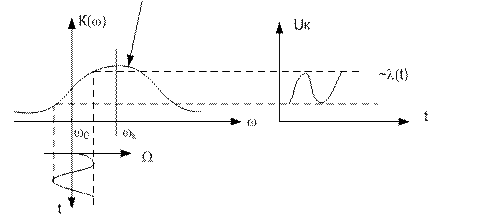
Рис.4.5работа детектора

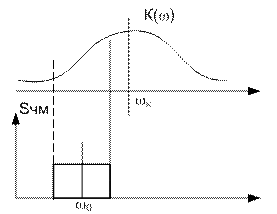
Рис.4.6спектр ЧМ и АЧХ контура

2. Демодулятор с ЧМ в ФМ + фазовое детектирование.

Фазовый детектор -> перемножитель напряжений + фильтр.

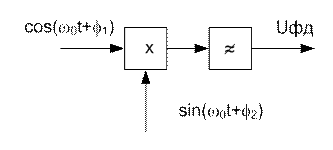
Рис.4.7модель фазового детектора

На выходе перемножителя:

cos (w_оt+f₁)sin(w_ot+f₂)= 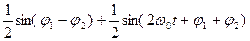(4.4)

после фильтра:

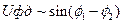~ Df (4.5)

[ фазовый детектор - двухвходовое устройство, выходное напряжение которого пропорционально разности фаз входных гармонических сигналов]

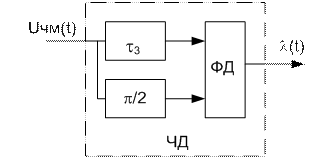
Рис.4.8модель ЧМ–ФМ-ФД

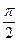-широкополосный фазовращатель;

τ₃ – линия задержки.

∆φ_t3=ωτ₃ (4.6)

ω_чм(t)=ω₀+ω_mλ(t) - изменение мгновенной частоты (4.7)

∆φ_лзчм=ω₀τ_з+ω_mτ_зλ(t) - задержка в верхней ветви (4.8)

Uв(t) = cos[ω₀t +ω₀τ_з+ω_mτ_зλ(t)] – напряжение на входе ФД верхнем

Uн(t) = sin[ω₀t + ω_mλ(t)] – напряжение на входе ФД нижнем

Uвых(t) = sin[ω₀τ_з + ω_m(1-τ_з)λ(t)] – напряжение на выходе ФД

Uвых(t) ~ ω_m (1-τ_з) λ(t) (4.9)

Линия сложна в реализации, поэтому используют колебательный контур

К(р)=е^-ptз

К(р)=М(p)/ N(p), m<n