Виды вибраций
В зависимости от характера колебаний различаются:
детерминированная вибрация:
- изменяется по периодическому закону;
- функция х(t), описывающая ее, изменяет значения через одинаковые интервалы времени Т (период колебания) и имеет произвольную форму (рис.3.1.а)
- если кривая x(t) изменяется с течением времени по синусоидальному закону (рис.3.1.б), то периодическая вибрация называется гармонической (в практике - синусоидальная). Для гармонической вибрации справедливо уравнение
x(t) = A sin (wt), (3.1)
где x(t) - смещение от положения равновесия в момент t;
А - амплитуда смещения; w = 2pf - угловая частота.
Спектр такой вибрации (рис.3.1. б) состоит из одной частоты f = 1/T.
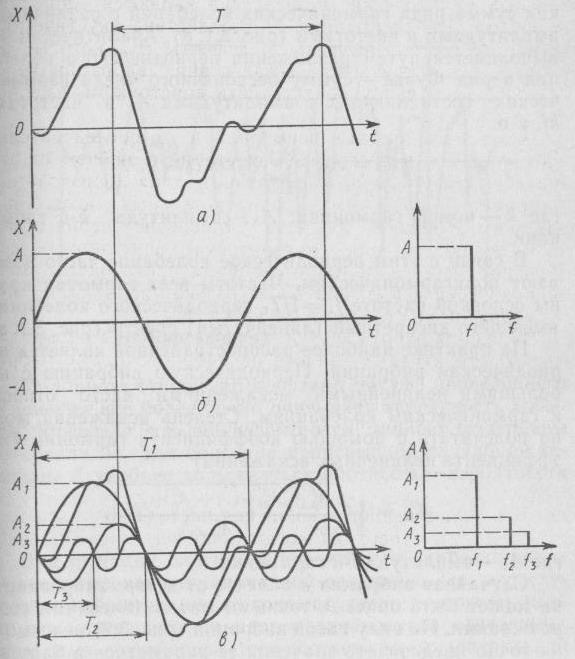
Рис.3.1. Периодическая вибрация (а); гармоническая вибрация и ее спектр частот (б); периодическая вибрация как сумма гармонических колебаний и ее спектр частот (в)
Полигармоническое колебание - частный вид периодической вибрации;:
- наиболее распространена на практике;
-периодическое колебание разложением в ряд Фурье может быть представлено как сумма ряда гармонических колебаний с различными амплитудами и частотами (рис.3.1.в).
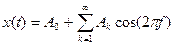
где k - номер гармоники;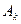 
- амплитуда k - й гармоники;
- частоты всех гармоник кратны основной частоте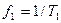 
периодического колебания;
- спектр является дискретным (линейчатым) и представлен на рис.3.1.в;
- ее часто относят с некоторыми искажениями к гармоническим колебаниям; степень искажения подсчитывается с помощью коэффициента гармоник
,
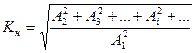где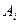 
- амплитуда i - гармоники.
Случайная вибрация:
- не может быть описана точными математическими соотношениями;
- невозможно предсказать точно значения ее параметров в ближайший момент времени;
- можно с определенной вероятностью предсказать, что мгновенное значение x(t) вибрации попадает в произвольно выбранный интервал значений от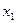 
до 
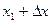(рис.3.2.).
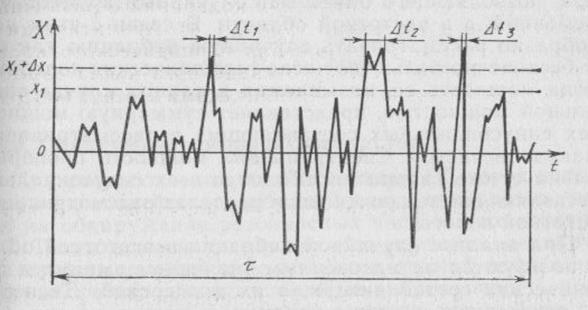
Рис.3.2. Случайная вибрация
Из рис.3.2. следует, что эта вероятность равна
,
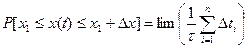где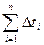 
- суммарная продолжительность нахождения амплитуды вибрации в интервале 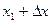за время наблюдения t.
Для описания непрерывной случайной величины пользуются плотностью вероятности:
- формула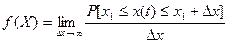 
;
- вид функции распределения характеризует закон распределения случайной величины;
-случайная вибрация – сумма множества независимых и мало отличающихся мгновенных воздействий (подчиняется закону Гаусса);
- вибрацию можно характеризовать:
математическим ожиданием М[X] – среднее арифметическое мгновенных значений случайной вибрации за время наблюдения;
генеральной дисперсией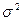 
- разброс мгновенных значений случайной вибрации относительно ее среднего значения.
- если колебательные процессы с одинаковыми M[X] и 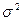отличаются друг от друга за счет различной частоты, то случайный процесс описывается в частотной области (случайная вибрация есть сумма бесконечно большого числа гармонических колебаний). Здесь используется спектральная плотность мощности случайной вибрации в полосе частот
,
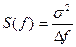где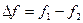 
- полоса частот.
Площадь под кривой зависимости спектральной плотности от частоты равна дисперсии амплитуд гармонических составляющих.
- среднее значение дисперсии случайной величины вибрации в полосе частот измеряется путем подачи этой вибрации на вход полосового фильтра с узкой полосой пропускания.
- «белый шум»: шумовой сигнал, частотный спектр которого постоянен и равномерен; его мощность постоянна в рассматриваемой полосе частот
Дата добавления: 2015-08-08; просмотров: 4195;