Вязкость. Движение жидкости в трубах
Все реальные жидкости и газы имеют внутреннее трение, которое также называется вязкостью. Вязкость является причиной постепенного прекращения движения жидкостей и газов после прекращения действия причин, его вызывающих.
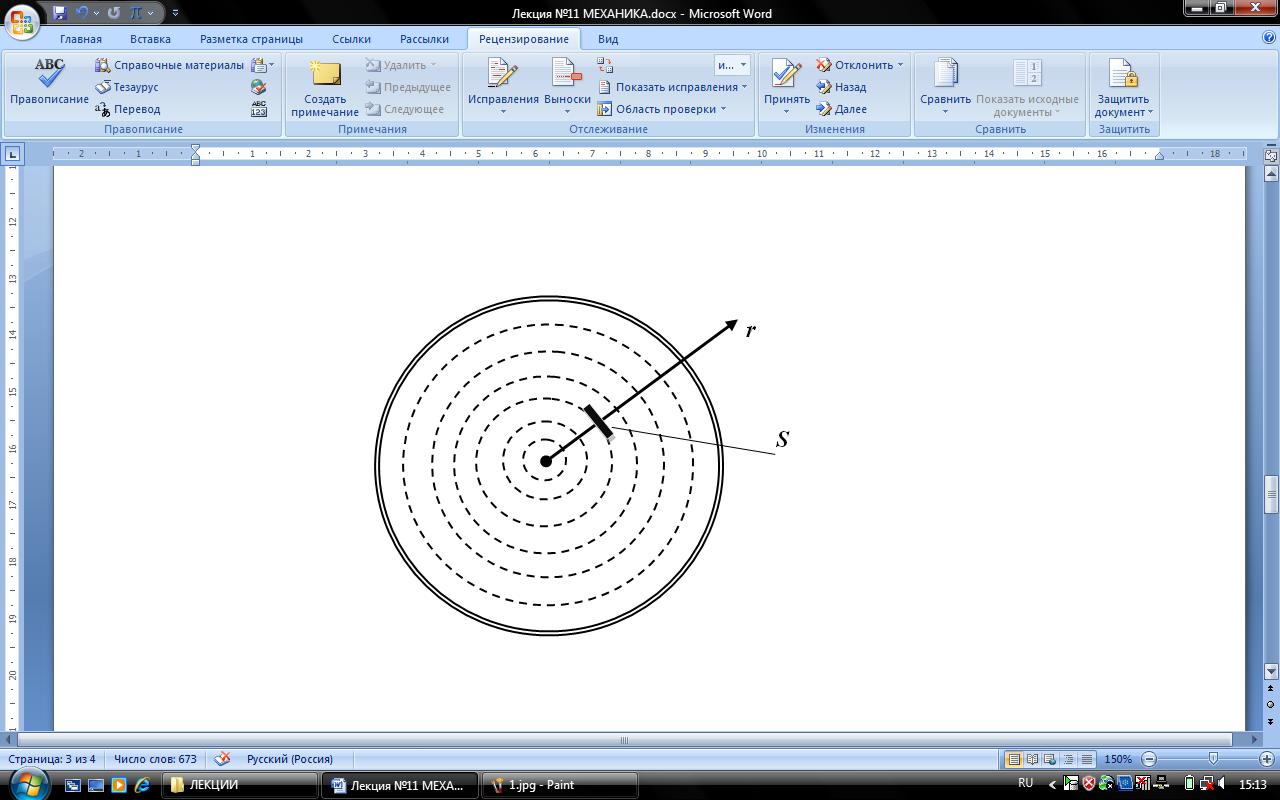 Измерения показывают, что при медленном течении скорость жидкости изменяется от нуля в непосредственной близости к стенкам трубы до максимальной на оси трубы. Жидкость при этом оказывается как бы разделённой на тонкие цилиндрические слои, которые скользят друг относительно друга не перемешиваясь. Такое течение называется ламинарным или слоистым (лат. lamina – пластинка, полоска).
Измерения показывают, что при медленном течении скорость жидкости изменяется от нуля в непосредственной близости к стенкам трубы до максимальной на оси трубы. Жидкость при этом оказывается как бы разделённой на тонкие цилиндрические слои, которые скользят друг относительно друга не перемешиваясь. Такое течение называется ламинарным или слоистым (лат. lamina – пластинка, полоска).
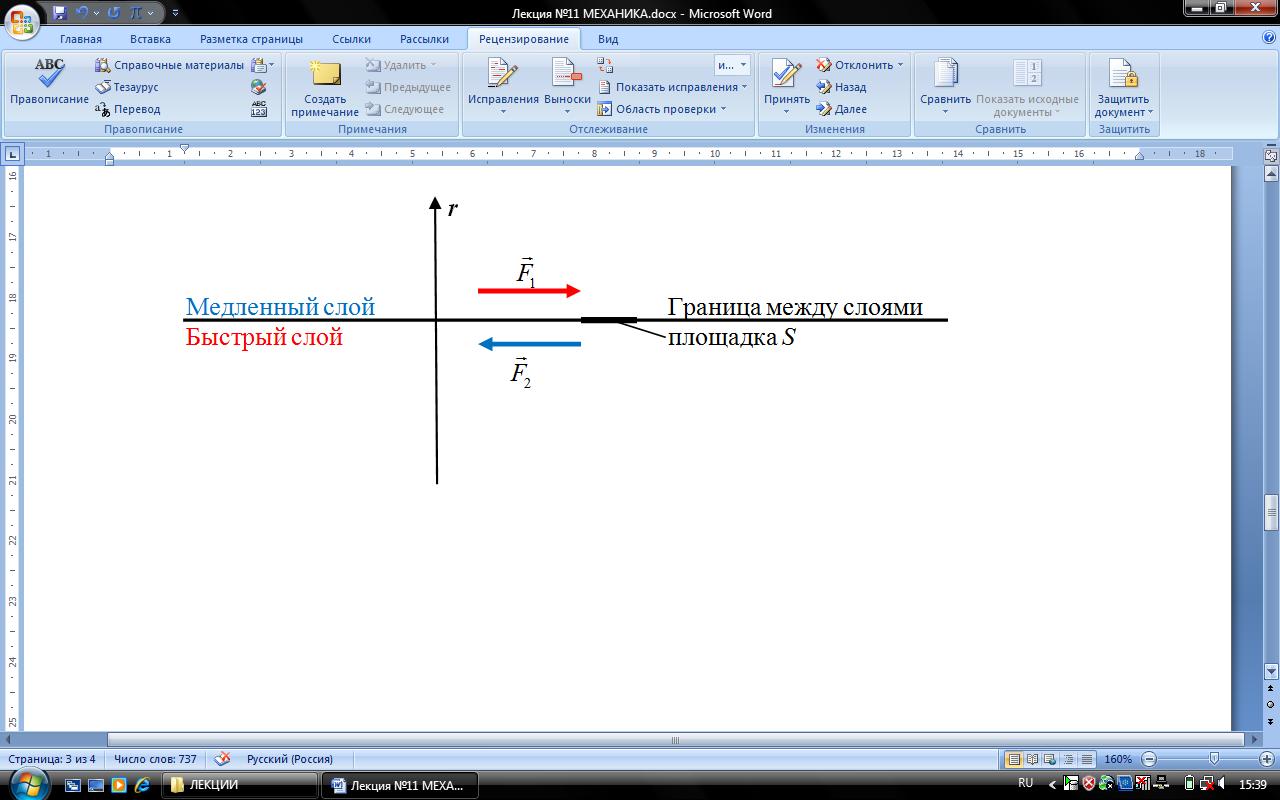 Из опыта известно, что для поддержки постоянного течения жидкости в трубе, необходимо наличие на концах трубы разности давлений. При стационарном течении жидкости без ускорения необходимость сил, обусловленных разным давлением на концах трубы, указывает на то, что эти силы уравновешиваются силами, тормозящими движение. Это силы внутреннего трения
Из опыта известно, что для поддержки постоянного течения жидкости в трубе, необходимо наличие на концах трубы разности давлений. При стационарном течении жидкости без ускорения необходимость сил, обусловленных разным давлением на концах трубы, указывает на то, что эти силы уравновешиваются силами, тормозящими движение. Это силы внутреннего трения 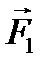 и
и 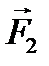 на границах между слоями жидкости, между жидкостью и стенками.
на границах между слоями жидкости, между жидкостью и стенками.
Для модуля силы внутреннего трения экспериментально установлено:
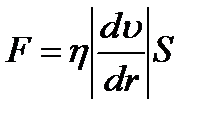 – закон Ньютона,
– закон Ньютона,
здесь: η – динамическая вязкость, 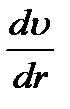 – производная, показывающая как быстро меняется в данном месте скорость в направлении, перпендикулярном к площадке S.
– производная, показывающая как быстро меняется в данном месте скорость в направлении, перпендикулярном к площадке S.
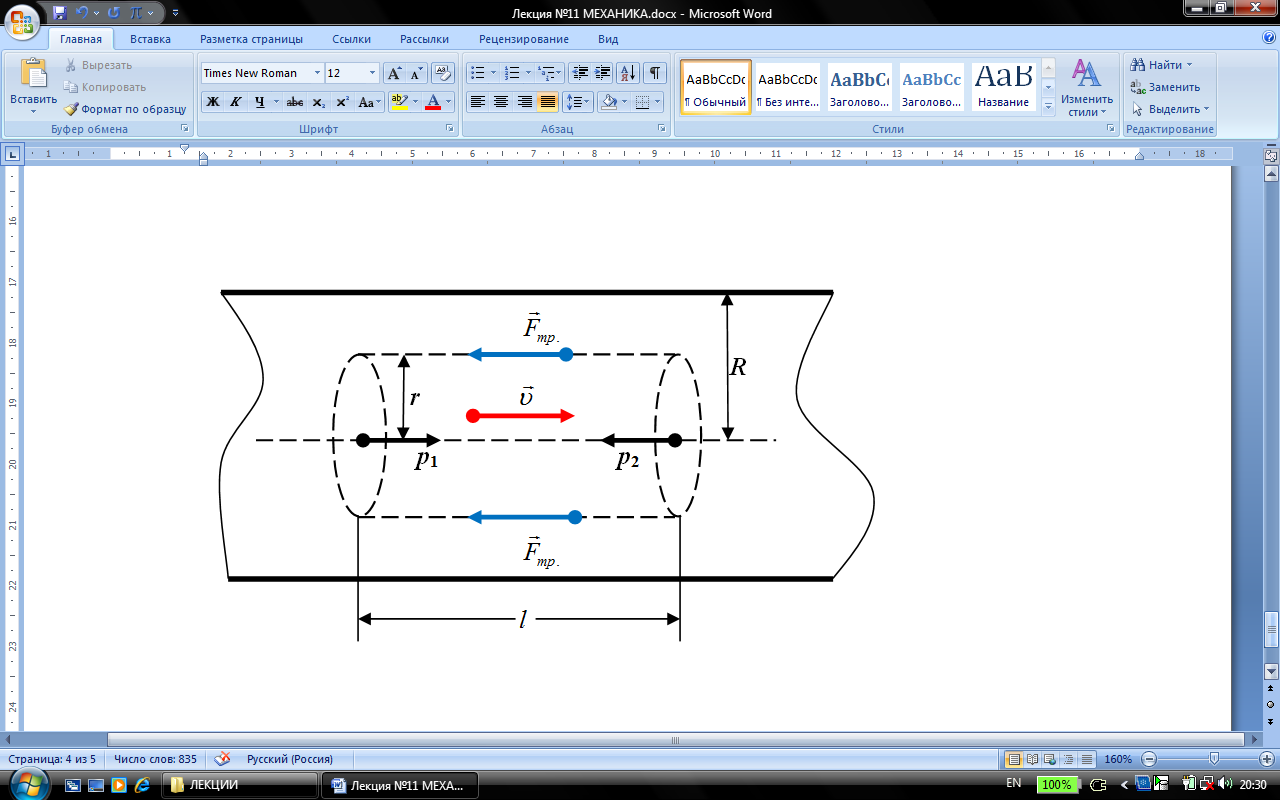 Найдём закон изменения модуля скорости слоёв жидкости при ламинарном течении и в трубе. Выделим воображаемый цилиндрический объём жидкости радиуса r и длины l. При стационарном течении ускорение этого объёма равно нулю. Следовательно: сумма сил, действующих на цилиндр равна нулю.
Найдём закон изменения модуля скорости слоёв жидкости при ламинарном течении и в трубе. Выделим воображаемый цилиндрический объём жидкости радиуса r и длины l. При стационарном течении ускорение этого объёма равно нулю. Следовательно: сумма сил, действующих на цилиндр равна нулю.
На цилиндр действуют в горизонтальном направлении:
- на основания цилиндра равнодействующая сил давления  ;
;
- на боковую поверхность сила вязкого трения  , где η – динамическая вязкость,
, где η – динамическая вязкость, 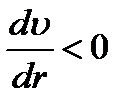 , т.к. скорость слоёв жидкости уменьшается в направлении возрастания r.
, т.к. скорость слоёв жидкости уменьшается в направлении возрастания r.
При стационарном течении Fдавл.=Fтр.. Следовательно 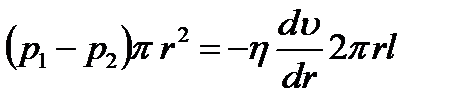 . Отсюда:
. Отсюда: 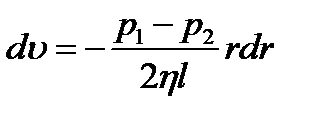 . В результате интегрирования:
. В результате интегрирования:  .
.
Постоянная С определяется из граничного условия υ|r=R=0:
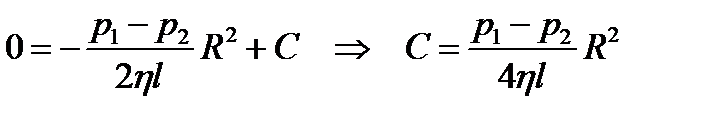 .
.
После подстановки: 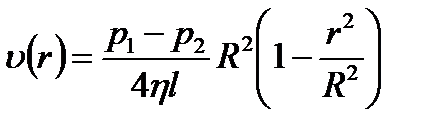 .
.
Скорость на оси трубы: 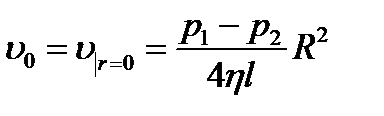 . Тогда:
. Тогда:
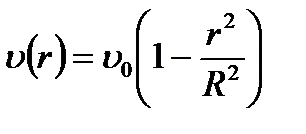 .
.
Дата добавления: 2015-08-08; просмотров: 1206;
