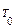Гармонические колебания. Рис. 1 Изучим простейшую колебательную систему –тело массы m, прикрепленное к пружине и скользящее без трения по горизонтальному столу (рис
|
 Изучим простейшую колебательную систему –тело массы m, прикрепленное к пружине и скользящее без трения по горизонтальному столу (рис. 1).
Изучим простейшую колебательную систему –тело массы m, прикрепленное к пружине и скользящее без трения по горизонтальному столу (рис. 1).
Рассмотрим движение этого грузика под действием однократно приложенной силы. Отклонение обозначим через х, и предположим, что имеем дело с абсолютно упругой пружиной. В этом случае пружина действует на груз с упругой силой F, пропорциональной смещению х и направленной в сторону обратную смещению, т. e. F= - kx, где k - коэффициент пропорциональности, называемый также жесткостью пружины. Знак "минус" означает, что сила упругости противодействует смещению.
В физике встречаются силы иного происхождения, чем упругие, которые обнаруживают такую же закономерность, т. е. оказываются равными -kx, где k – постоянная положительная величина.
Силы такого вида, независимо от их природы, принято называть квазиупругими.
Под действием этой однократно приложенной силы грузик начнет совершать колебания.
Механическая система, совершающая колебания около положения равновесия, называется классическим осциллятором.
Промежуток времени, по истечению которого движение повторится, называется периодом колебания и обозначается Т, [Т] = с.
Частота колебаний равна числу полных колебаний за 1 с: 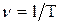 . Частота измеряется в Гц. 1 Гц - это одно колебание за 1 с. В технике частоты измеряются также в килогерцах (1 кГц = 103 Гц), мегагерцах (1 Мгц = 106 Гц), гигагерцах (1ГГц = 109 Гц ).
. Частота измеряется в Гц. 1 Гц - это одно колебание за 1 с. В технике частоты измеряются также в килогерцах (1 кГц = 103 Гц), мегагерцах (1 Мгц = 106 Гц), гигагерцах (1ГГц = 109 Гц ).
Выведем уравнение колебаний гармонического осциллятора.
Напишем 2-й закон Ньютона: F = та, где F = -kx, а ускорение 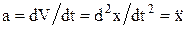 . В итоге получаем
. В итоге получаем 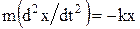 или
или
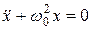 , (1)
, (1)
где 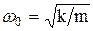 . (2)
. (2)
Уравнение (1) является обыкновенным линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Его решением будет:
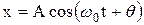 или
или 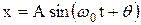 , (3)
, (3)
где А - амплитуда колебаний, т. е. наибольшее отклонение колеблющегося грузика от положения равновесия; оно задается начальными условиями при однократном приложении силы.
Поскольку значения как cos так и sin через 2p радиан повторяются, то можно найти связь между периодом Т0 и 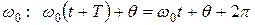 , откуда
, откуда

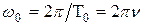 (4)
(4)
|
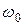 - называется собственной круговой частотой. Она равна числу полных колебаний за
- называется собственной круговой частотой. Она равна числу полных колебаний за 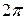 секунд. Для вращательного движения круговая частота и величина угловой скорости
секунд. Для вращательного движения круговая частота и величина угловой скорости 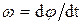 совпадают.
совпадают.
|
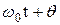 в скобках (3) называют фазой колебания. Она определяет смещение в данный момент времени t;
в скобках (3) называют фазой колебания. Она определяет смещение в данный момент времени t; 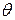 – начальная фаза. Она характеризует смещение в начальный момент времени t = 0 и определяется начальными условиями, как и амплитуда А.
– начальная фаза. Она характеризует смещение в начальный момент времени t = 0 и определяется начальными условиями, как и амплитуда А.
|
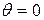 , тогда
, тогда 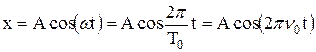 .
.
График этого уравнения приведен на рис. 2. Из (2) и (4) следует, что период колебания 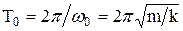 не зависит от амплитуды колебаний А.
не зависит от амплитуды колебаний А.
Скорость 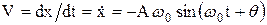 (5)
(5)
пропорциональна амплитуде и круговой частоте, и отличается по фазе от смещения (3) на 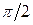 . Максимальная скорость
. Максимальная скорость 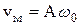 .
.
Ускорение 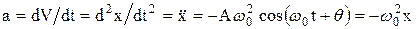 (6)
(6)
пропорционально A и 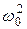 , и по направлению совпадает с направлением силы
, и по направлению совпадает с направлением силы 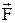 , а по фазе отличается от скорости (6) на
, а по фазе отличается от скорости (6) на 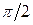 , и от смещения (3) – на
, и от смещения (3) – на 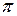 . Максимальное ускорение
. Максимальное ускорение 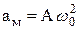 .
.
Простейшее периодическое колебание, при котором смещение изменяется со временем по закону cos или sin называется гармоническим колебанием.
Как следует из (5) и (6) скорость и ускорение колеблющегося груза изменяется со временем также по гармоническому закону, т. е. по закону sin и cos.
Дата добавления: 2015-08-08; просмотров: 645;