V. Демпфирование.
Общий вид динамического уравнения движения:
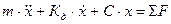 (1)
(1) 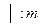
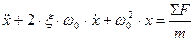 (2)
(2)
где ξ – относительный коэффициент демпфирования.
Общее решение дифференциального уравнения (2) будем искать в виде суммы вынужденной и свободной составляющих:
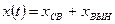
Вначале определим свободную составляющую решения. Для этого запишем характеристическое уравнение, соответствующее дифференциальному уравнению (2):
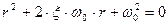
и найдем его корни:
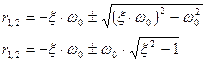
В случае 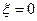 уравнение (2) приобретает вид:
уравнение (2) приобретает вид:
 ,
,
а корни его характеристического
уравнения:
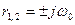
Таким корням характеристического уравнения соответствует следующее решение дифференциального уравнения:
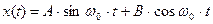
Константы А и В можно определить из начальных условий: 
Подставляя найденные значения констант в выражение для x(t), получим свободную составляющую решения дифференциального уравнения (2):
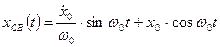
|
Вынужденная составляющая решения уравнения (2) определяется выражением:
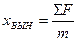

x(t)
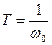 t
t
В случае 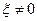 корни характеристического уравнения определяются соотношением:
корни характеристического уравнения определяются соотношением:
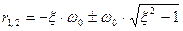
Проанализируем последнее выражение:
В случае 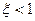 корни комплексно-сопряженные.
корни комплексно-сопряженные.
В случае 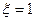 корни действительные, равные.
корни действительные, равные.
В случае 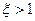 корни действительные, не равные.
корни действительные, не равные.
Рассмотренным значениям относительного коэффициента демпфирования соответствуют следующие свободные составляющие решения уравнения (2):
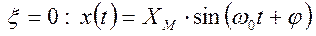 ;
;
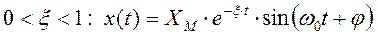
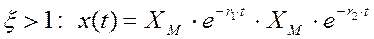
В случае 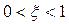 переходный процесс колебательный:
переходный процесс колебательный:
 X(t)
X(t)
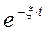


 XУCT
XУCT
 t
t
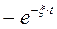

Т
В случае 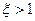 переходный процесс апериодический, причем с увеличением демпфирования замедляется темп процессов:
переходный процесс апериодический, причем с увеличением демпфирования замедляется темп процессов:

 |  |

 ХУСТ
ХУСТ
0 t
При наличии демпфирования 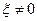
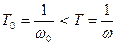 , где
, где
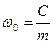 ,
, 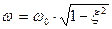 .
.
1. Критерии выбора относительного коэффициента демпфирования.
Время переходного процесса:
Теоретически время переходного процесса бесконечно, но на практике оно определяется как момент вхождения процесса в заданную трубку точности.
 Х
Х





 ХУСТ
ХУСТ


t
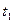
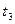
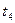
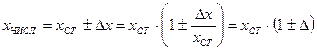
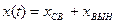

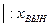
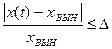
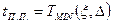
Дата добавления: 2015-08-04; просмотров: 792;
