Приборы, в которых изучаются законы образования газов при горении пороха в постоянном объеме называются манометрическими бомбами.
Наиболее распространенной до настоящего времени являлась бомба Вьеля. Бомба (рис. 9) состоит из полого толстостенного цилиндра А из высокопрочной стали (обычно из ОХНЗМФА) с винтовой нарезкой на обоих концах внутренней поверхности. С одной стороны ввинчивается запальная втулка В, с другой – поршневая втулка G (обычно с крекерным манометром). В запальной втулке имеется изолированный стержень для подведения электрического тока, воспламеняющего запал. Второй провод подводится непосредственно к телу бомбы. Проволочка, соединяющая борны С и С1 и пережигаемая затем током, проходит через гильзу из папиросной бумаги, в которой помещается определенная навеска воспламенителя (черный порох, пироксилиновая вата).
Таблица 11
| P,атм. | T0 ,0C | U0, см/c | Хп,мк | l20,мк | t1,МСЕК | t2,мсек |
| 0,0 | 0,34 | 10,30 | 0,12 | |||
| 0,67 | 3,42 | 0,11 | ||||
| 1,06 | 110* | 1,89 | 0,16 |
где l20 для р=100 атм. Приведен для всей газовой зоны
t2- также для всей газовой зоны при р=100 атм.
Из таблицы 11 видно что время t1>>t2 ,т. е газовую зону горения можно считать полностью «безынерционной» по сравнению с прогретым слоем пороха .
Из данных таблицы 10 видно , что реакция газификации пороха является экзотермической реакцией. Тем не менее этого тепла недостаточно для поддержания стационарного горения , по этому необходим дополнительный приток тепла из газа .Причиной этого может быть диспергирование пороха , при котором реагирующее вещество выносится из зоны газификации . По экспериментальным данным П. Ф. Похила % диспергирования может быть высоким ( до 70 % от всего вещества ). Если бы диспергирования не было бы то расчеты выполненные А. Г. Мергияновым показывают, что скорость горения могла бы достигнуть 250 см/сек.
3.2 формула для наибольшего давления газов.
Произведя большое количество опытов , нанеся значение наибольшего давления Pm и плотность заряжания D на график , проводя по полученным точкам кривую Pm , D и подбирая уравнение этой кривой Нобль и Абель установили следующую эмпирическую зависимость между плотностью заряжания D и наибольшим давлением Pm :
Pm=f×D/(1-a×D) (3.1)
В этой формуле f и a - постоянные коэффициенты , определяемые из ряда опытов при разных D . Величину f назвали «силой» пороха , a- коволюмом.
Правильный физический смысл f и a выясняется при сопоставлении формулы
(3.1) с уравнением Ван-дер-Вальса для реального газа в упрощенном виде
(а/w2<<р).
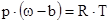 (3.2)
(3.2)
где b-характеристика объема молекул .
Если в объеме W0 сгорит w кг пороха , целиком превратившегося в газы , температура которых равна температуре горения Т1 , то уравнение (3.2) можно записать
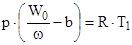
или
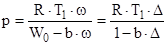 (3.3)
(3.3)
Сравнивая формулы (3.1) и (3.3) получим 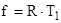 , b=a.
, b=a.
Т.к. 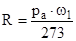 - есть работа , которую совершает 1 кг газа , если его нагреть на 1 градус при атмосферном давлении . Следовательно f - есть работа 1 кг пороховых газов , которую он мог бы совершить , расширяясь изобарно при нагревании на T1 , К при p=pа=103.3 кг/дм2 . a=b - есть поправка на собственный объем молекул , названная коволюмом
- есть работа , которую совершает 1 кг газа , если его нагреть на 1 градус при атмосферном давлении . Следовательно f - есть работа 1 кг пороховых газов , которую он мог бы совершить , расширяясь изобарно при нагревании на T1 , К при p=pа=103.3 кг/дм2 . a=b - есть поправка на собственный объем молекул , названная коволюмом 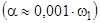 .
.
Величины f и a зависят от природы пороха . Строго говоря , f и a зависят от давления . С увеличением давления a монотонно уменьшается но не может быть меньше 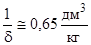 .
.
3.3 Определение силы пороха и коволюма пороховых газов .
Величины f и a можно определить аналитически и графически . Имеем линейное уравнение с двумя постоянными коэффициентами f и a .
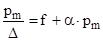 (3.1/)
(3.1/)
Чтобы найти f и a достаточно знать два значения pm при разных плотностях заряжания D . Окончательно получим
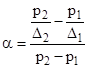 (3.4)
(3.4)
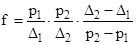 (3.5)
(3.5)
Чтобы , точность определения f и a из опытов была выше , необходимо чтобы разность плотностей заряжания была по возможности наибольшей .
Наименьшая плотность заряжания соответствует примерно 0,1 кг/дм3 , при которой обеспечивается максимальное давление 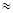 1000 кг/см2 . Значение давления 1000 кг/см2 есть нижнее значение при котором сохраняется линейность изменения скорости горения пороха от давления .
1000 кг/см2 . Значение давления 1000 кг/см2 есть нижнее значение при котором сохраняется линейность изменения скорости горения пороха от давления .
Верхнее значение плотности заряжания ограничено прочностью бомбы . Как правило прочность бомбы не превосходит 4000 кг/см2 , по этому рекомендуется проводить испытания при следующих значениях плотностей заряжания :
для пироксилиновых порохов D1=0.15 кг/дм3 и D2=0.25 кг/дм3 .
для нитроглицириновых - D1=0.12 кг/дм3 и D2=0.20 кг/дм3 .
Относительная погрешность определения f и a определяется по известной формуле
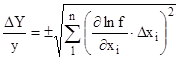 (3.6)
(3.6)
где 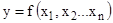 .
.
x1,x2,xn - измеряемые величины .
В нашем случае измеряемые величины давление - p , навеска пороха - w и объем манометрической бомбы W0 .
Представив формулы для f и a в виде
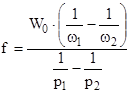 (3.7)
(3.7)

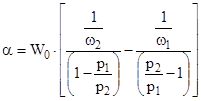 (3.8)
(3.8)
Получим
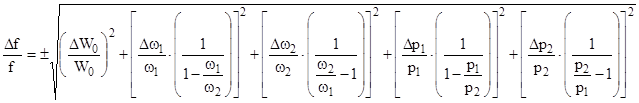
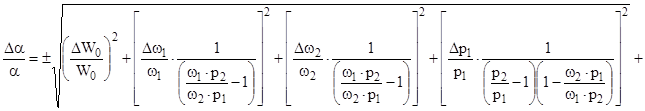 Полагая , что измерения имели относительную ошибку в 1%
Полагая , что измерения имели относительную ошибку в 1%
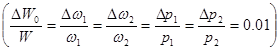
p2=3000 , p1=1000 , т.е. 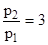
 ,
, 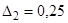 , D1=0,15
, D1=0,15
Получим
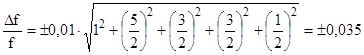 .
.
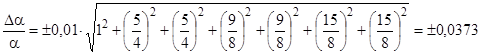 .
.
Как видно из вычислений при измерении величин w , W0 и p с точностью 1% относительная ошибка в определении f будет 3,5% , а a - 3,7% .
Чтобы повысить точность f и a необходимо повысить точность взвешивания и измерения давления , особенно на нижних их пределах
(w1 и p1) .
3.4 Давление в промежуточный момент . Общая формула пиростатики .
Формула Нобля относится к моменту достижения максимального давления , когда порох сгорит . Для промежуточного момента , когда сгорела только его часть  сг=
сг=  ( где
( где 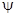 - относительная часть сгоревшего пороха ) , воспользуемся уравнением состояния в форме Дюпре
- относительная часть сгоревшего пороха ) , воспользуемся уравнением состояния в форме Дюпре
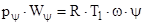 (3.11)
(3.11)
где py - давление в момент , когда сгорела относительная часть заряда - y .
Wy - свободный объем бомбы в данный момент . Он равен :
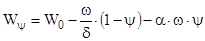 (3.12)
(3.12)
где W0 - объем бомбы ,
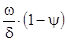 - объем несгоревшего пороха ,
- объем несгоревшего пороха ,
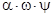 - поправка на объем молекул сгоревшего пороха .
- поправка на объем молекул сгоревшего пороха .
Подставляя значения Wy в уравнение (3.11) и учитывая , что 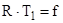
окончательно получим 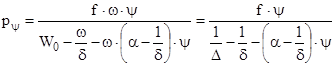 (3.13)
(3.13)
где 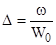 - плотность заряжания ,
- плотность заряжания ,
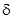 - удельный вес пороха ,
- удельный вес пороха ,
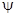 - относительная часть сгоревшего пороха ,
- относительная часть сгоревшего пороха ,
 - коволюм .
- коволюм .
При 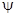 =1 получаем формулу Нобеля
=1 получаем формулу Нобеля
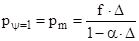 ;
;
На практике важно знать какая часть сгорела порохового зерна при достижении заданного давления . Из формулы (3.13) имеем 
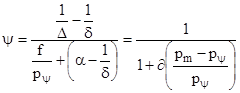 (3.14)
(3.14)
где 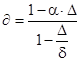 - постоянная величина для данного опыта и представляющая собой отношение свободного объема бомбы в конце горения
- постоянная величина для данного опыта и представляющая собой отношение свободного объема бомбы в конце горения 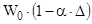
к свободному объему в начале горения 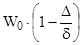 .
.
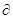 всегда < 1 . С уменьшением
всегда < 1 . С уменьшением 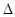
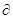 приближается к 1 .
приближается к 1 .
3.5 Учет влияния воспламенителя .
В опытах Нобля с дымным порохом воспламенителем служил дымный порох и при расчете плотности заряжания вес воспламенителя включался в общий вес заряда . При работе с бездымными порохами в манометрической бомбе или в орудии учет давления воспламенителя необходим .
Обозначим вес заряда воспламенителя через 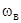 , силу воспламенителя через fв и коволюм газов воспламенителя через
, силу воспламенителя через fв и коволюм газов воспламенителя через  в .
в .
Тогда в момент сгорания воспламенителя и зажжения пороха давление газов воспламенителя будет
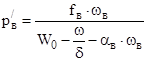
В промежуточный момент
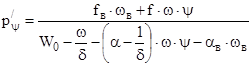
В конце горения
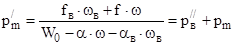 ,
,
где 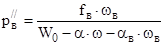 ,
, 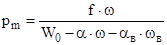 ,
,
т.к. значение 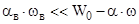 коволюмом воспламенителя можно пренебречь и ,учитывая , что 1-
коволюмом воспламенителя можно пренебречь и ,учитывая , что 1- 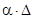 < 1-
< 1- 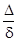 (
( 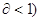 ,
,
то 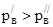 . Можно принять
. Можно принять 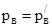 при расчете давлений , т.е. несмотря на разницу
при расчете давлений , т.е. несмотря на разницу 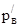 и
и 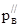 в 10% само значение pв составляет 10-20% от общего давления пороховых газов . По этому такое допущение оправдано . Окончательно будем иметь :
в 10% само значение pв составляет 10-20% от общего давления пороховых газов . По этому такое допущение оправдано . Окончательно будем иметь :
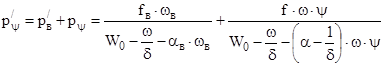 (3.15)
(3.15)
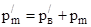
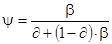 (3.16)
(3.16)
где 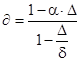 ;
; 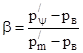
Зная изменение давления по времени 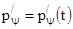 находим
находим 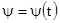 .
.
Зная закон изменения 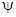 по времени можно найти также опытный закон изменения
по времени можно найти также опытный закон изменения 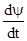 т.е. быстроту газообразования . Эта величина является одной из важнейших характеристик , знание которых позволяет регулировать приток газа при горении пороха и управлять законом изменения давления газов .
т.е. быстроту газообразования . Эта величина является одной из важнейших характеристик , знание которых позволяет регулировать приток газа при горении пороха и управлять законом изменения давления газов .
3.6 Учет потерь на теплоотдачу стенкам бомбы при горении пороха в замкнутом объеме .
При горении пороха в замкнутом объеме , часть энергии пороховых
газов тратится на нагрев стенок бомбы и следовательно давление газов будет ниже , чем расчетное без учета теплоотдачи . Эти потери на теплоотдачу зависят от ряда условий .
Первые опыты профессора С.П. Вуколова , проведенные еще в 1895 - 96 гг. При 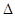 =0.2 кг/дм3 показали значительную разницу в давлениях pm в обычной манометрической бомбе и в бомбе , внутренняя поверхность которой покрыта тонким слоем слюды , плохо проводящей тепло .
=0.2 кг/дм3 показали значительную разницу в давлениях pm в обычной манометрической бомбе и в бомбе , внутренняя поверхность которой покрыта тонким слоем слюды , плохо проводящей тепло .
Без слюды pm=2033 кг/см2 , со слюдой pm=2202 кг/см2 т.е. разница составляла около 8% . Такая разница в давлениях несомненно должна отразиться на расчете баллистических характеристик . Первая попытка экспериментально получить и теоретически обосновать поправочные зависимости для учета потерь на теплоотдачу принадлежит французкому исследователю Мюрауру . По мнению Мюраура потеря на теплоотдачу пропорциональна охлаждающей поверхности Sб бомбы , давление газов p и времени действия их на стенку - t , т.е. числу ударов молекул газа о стенку .


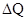 ~
~ 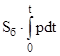
т.к. 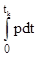 не зависит от
не зависит от 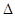 , что подтвердил Мюраур при разных
, что подтвердил Мюраур при разных  , то для данной бомбы и данного пороха потеря тепла не зависит от навески пороха
, то для данной бомбы и данного пороха потеря тепла не зависит от навески пороха 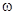 . Тогда относительные потери тепла
. Тогда относительные потери тепла
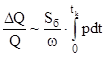 (3.17)
(3.17)
т.к. 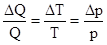 при постоянном объеме , то
при постоянном объеме , то
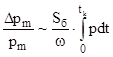 (3.18)
(3.18)
Для количественного определения потерь на теплоотдачу Мюраур проводил опыты в бомбе объемом W0 = 150 см3 , при 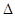 = 0.2 кг/дм3 .
= 0.2 кг/дм3 .
Один раз порох сжигал без вставки и получил давление p1 . Другой раз вставлял в бомбу корытообразный вкладыш ( рис.13 ) ( фиг.17 ) , который обмывался пороховыми газами со всех сторон.
Вкладыш был из того же материала, что и бомба. Было получено давление P2 .
В первом случае поверхность была Sб , во втором случае Sб + Sвкл. Разница в давлении 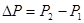 была за счёт дополнительной поверхности Sвкл. Тогда поправка на давление -
была за счёт дополнительной поверхности Sвкл. Тогда поправка на давление - 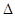 P' за счёт теплоотдачи в первом случае будет равна:
P' за счёт теплоотдачи в первом случае будет равна:
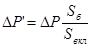 (3.19)
(3.19)
И давление Р1'=P1+ 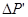 ,будет давление при Sб=0, т.е. получается таким, как в случае отсутствия потерь на теплоотдачу. Зная P1 и
,будет давление при Sб=0, т.е. получается таким, как в случае отсутствия потерь на теплоотдачу. Зная P1 и 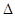 P' Мюреур определил относительную поправку на теплоотдачу
P' Мюреур определил относительную поправку на теплоотдачу 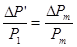
Такие опыты с большим количеством порохов разной толщины и природы установили важную зависимость 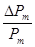 % от времени сгорания пороха при
% от времени сгорания пороха при 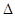 =0,2кг/дм3,причём в этих опытах
=0,2кг/дм3,причём в этих опытах 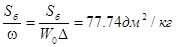 .
.
Опыты проводим с цилиндрическими крешерами при давлении воспламенителя Pв=250кг/см2 .Полученные данные 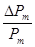 % или
% или 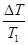 % были нанесены на график в функции времени сгорания tk . Полученная кривая названа "кривой C" (рис.14) (фиг.18) . Для определения потери на теплоотдачу в других условиях надо с начало испытать порох при навеске
% были нанесены на график в функции времени сгорания tk . Полученная кривая названа "кривой C" (рис.14) (фиг.18) . Для определения потери на теплоотдачу в других условиях надо с начало испытать порох при навеске 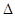 =0,2кг/дм3 и Pв=250кг/дм2 ,найти время сгорания tk и по tk войти в график(рис.14) , определить Cм%=
=0,2кг/дм3 и Pв=250кг/дм2 ,найти время сгорания tk и по tk войти в график(рис.14) , определить Cм%= 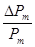 %. Потеря же в других условиях: других бомбах и другой плотности заряжания найдется по формуле:
%. Потеря же в других условиях: других бомбах и другой плотности заряжания найдется по формуле:
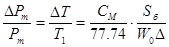 (3.20),
(3.20),
где Sб -в дм2, W0-в дм3, 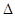 -в кг/дм3.
-в кг/дм3.
При проведении опытов с плотностью заряжания 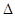 =0,2 кг/дм3 необязательно применять Pв=250кг/cм2 практически мгновенное воспламенение получается уже при Pв=(100-120)кг/cм2 2 .Чтобы войти в график (рис 14) достаточно откорректировать время сгорания пороха – tк,:
=0,2 кг/дм3 необязательно применять Pв=250кг/cм2 практически мгновенное воспламенение получается уже при Pв=(100-120)кг/cм2 2 .Чтобы войти в график (рис 14) достаточно откорректировать время сгорания пороха – tк,:
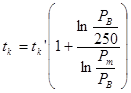 (3.21)
(3.21)
В таблице 12 приведены результаты подсчетов по графику для пороха с постоянной поверхностью горения.
Значения коэффициента CМ% для пироксилиновых порохов
Таблица 12
| толщина 2е1 | 0,3 | 0,3флегмат | 0,4 | 1,0 | 2,0 | 4,0 |
| скорость горения U1*107 дм/сек:кг/дм2 | ||||||
коэффициент 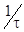
| ||||||
время сгорания в мсек при  кг/дм3 и РВ=250кг/см2 кг/дм3 и РВ=250кг/см2
| 1,76 | 2,26 | 2,64 | 7,0 | 14,6 | 31,0 |
| коэффициент теплопередачи СМ% | 1,5 | 2,0 | 2,6 | 4,0 | 5,0 | 6,1 |
где 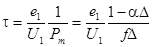 ;
; 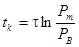
Рассмотрим пример с использованием таблицы 12. Имеется бомба W0=78.5cм3 и 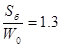 см2/см3. Проведены опыты с порохом толщиной 1 мм при
см2/см3. Проведены опыты с порохом толщиной 1 мм при 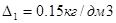 и
и 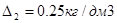 получим давление Рm1=1435кг/см2 и Рm2=2760кг/см2 . Рm2 - Рm1 =1325кг/см2 , определяем
получим давление Рm1=1435кг/см2 и Рm2=2760кг/см2 . Рm2 - Рm1 =1325кг/см2 , определяем 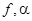 без учета потерь на теплоотдачу
без учета потерь на теплоотдачу 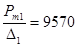 ;
; 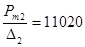 ;
; 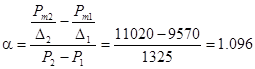 дм3/кг
дм3/кг 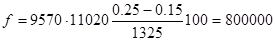 кгдм/кг .
кгдм/кг .
Введем поправку в давление Рm1 и Рm2 на теплоотдачу и определим исправленные значения если 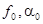 :
: 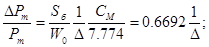
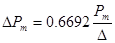 (по таблице СМ%=4%)
(по таблице СМ%=4%)
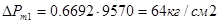
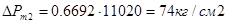
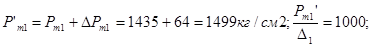
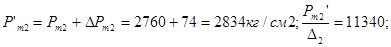
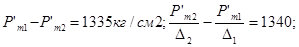
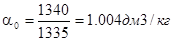
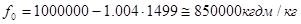
Дата добавления: 2015-07-06; просмотров: 2144;
