Теоретическое обоснование. Частотные методы основаны на привычном для инженеров графическом изображении динамических характеристик
Частотные методы основаны на привычном для инженеров графическом изображении динамических характеристик, которые можно снять экспериментально, поэтому они находят широкое применение. В частности зная АФЧХ разомкнутой САУ Wp(j  ), можно построить АФЧХ замкнутой САУ
), можно построить АФЧХ замкнутой САУ
Wз(j  ) =
) = 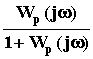 = Pз(
= Pз(  ) + jQз(
) + jQз(  ),
),
а по ней - требуемую для частотных методов вещественную ЧХ замкнутой САУ Pз(  ). Зная ВЧХ замкнутой САУ, можно приближенно построить переходную характеристику САУ h(t), которую снять экспериментально очень трудно, и по ней определить показатели качества управления.
). Зная ВЧХ замкнутой САУ, можно приближенно построить переходную характеристику САУ h(t), которую снять экспериментально очень трудно, и по ней определить показатели качества управления.
Теоретическое обоснование этого в том, что любую функцию, в том числе и единичную ступенчатую, можно разложить в ряд Фурье:
1(t) = A0 + 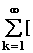 Ak1cos(k
Ak1cos(k  t) + Ak2sin(k
t) + Ak2sin(k  t)].
t)].
Так как замкнутая САУ линейна, то при подаче на вход суммы сигналов с выхода снимается сигнал, равный сумме реакций на каждый из входных сигналов. Входному сигналу ui(wi,t) на выходе будет соответствовать составляющая выходного сигналаyi(  i,t) = W(j
i,t) = W(j  i)
i) 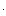 ui(
ui(  i,t), тогда
i,t), тогда
h(t) = 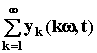 = A0W(0) +
= A0W(0) + 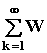 (jkw)
(jkw) 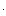 [Ak1cos(kwt) + Ak2sin(kwt)].
[Ak1cos(kwt) + Ak2sin(kwt)].
Преобразование этого выражения приводит к двум равнозначным формулам определения h(t) через составляющие ВЧХ:
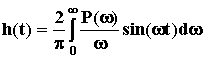 ;
; 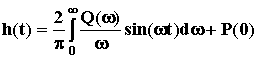 ,
,
где P(  )и Q(
)и Q(  ) - вещественная и мнимая части АФЧХ замкнутой САУ. Предпочтение обычно оказывают первой формуле, хотя с одинаковым успехом можно использовать и вторую.
) - вещественная и мнимая части АФЧХ замкнутой САУ. Предпочтение обычно оказывают первой формуле, хотя с одинаковым успехом можно использовать и вторую.
Точно вычислить эти интегралы можно только с помощью ЭВМ, но в практике нашел широкое применение приближенный способ построения переходной характеристики на основе линейной аппроксимации ВЧХ замкнутой САУ, который называется метод трапеций. Прежде, чем рассматривать этот метод, рассмотрим без доказательства основные соотношения между ВЧХ замкнутой САУ и ее переходной характеристикой.
Дата добавления: 2015-07-24; просмотров: 971;
