Приклад.

Знайти градієнт функції 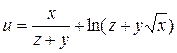в точці М(1,2,1).

ПОХІДНА ФУНКЦІЇ ЗА НАПРЯМОМ ВЕКТОРА

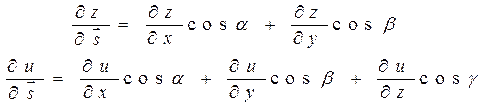
ПРИКЛАД

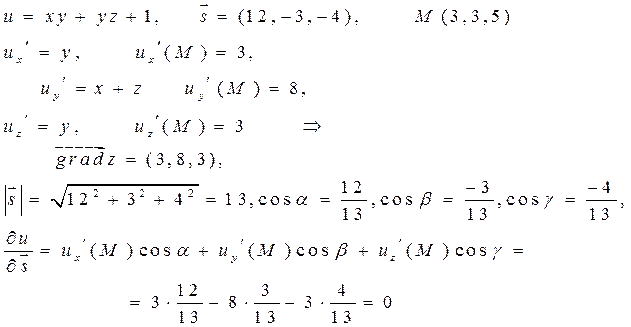
Приклад:

Знайти похідну функції 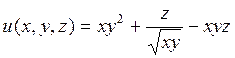в точці М(1,2,1) в напрямі, який утворює з осями координат кути відповідно .

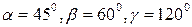ЧАСТИННІ ПОХІДНІ ДРУГОГО ПОРЯДКУ

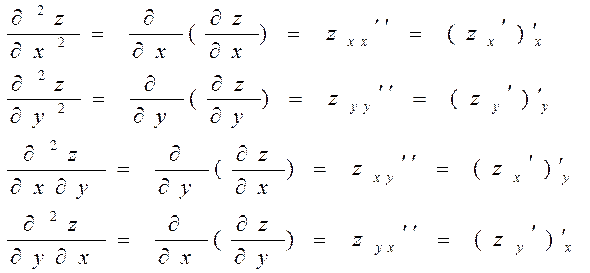
ПОВНІ ДИФЕРЕНЦІАЛИ ДРУГОГО ПОРЯДКУ

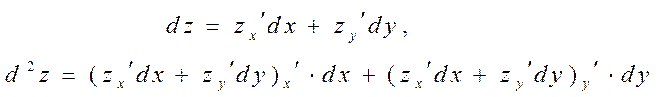
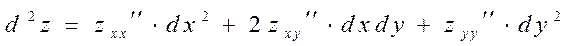
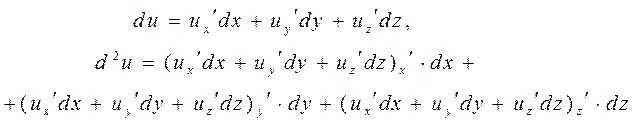
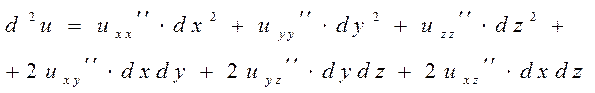
ЕКСТРЕМУМИ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ

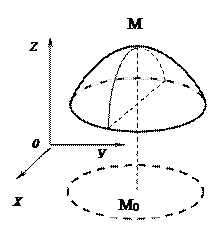
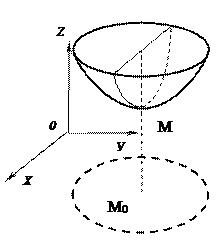
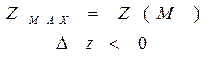
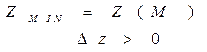
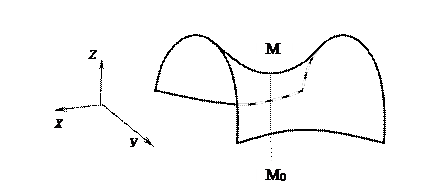
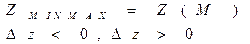
НЕОБХІДНІ УМОВИ ЕКСТРЕМУМА

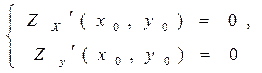
ДОСТАТНІ УМОВИ ЕКСТРЕМУМУ

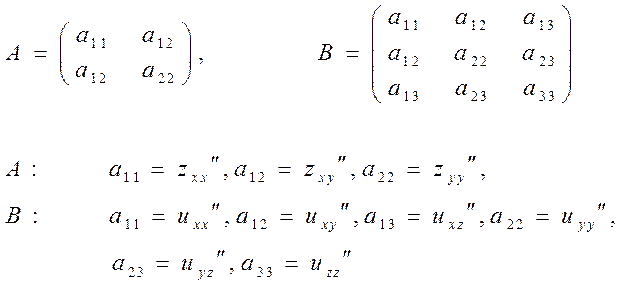
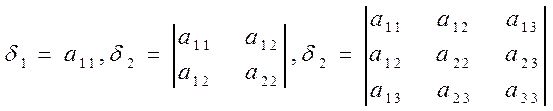
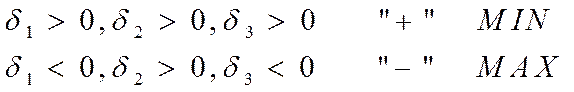
ПРИКЛАД

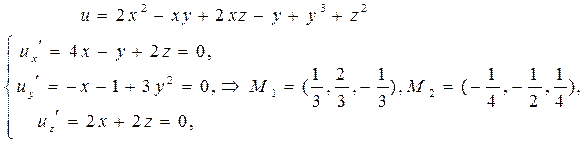
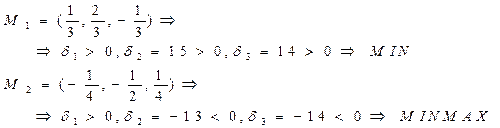
Приклад:

Знайти екстремум функції: = .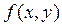

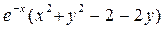УМОВНИЙ ЕКСТРЕМУМ ФУНКЦІЇ ДВОХ ЗМІННИХ

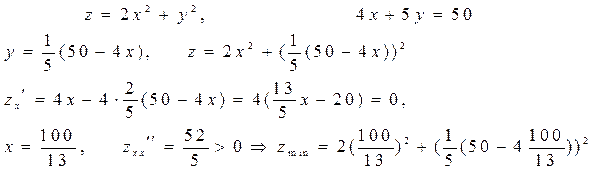
Приклад:

Знайти екстремум інвестиційної функції 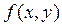= 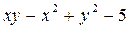при умові рівноваги 3 .

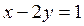УМОВНИЙ ЕКСТРЕМУМ ФУНКЦІЇ ДВОХ ЗМІННИХ. МЕТОД ЛАГРАНЖА

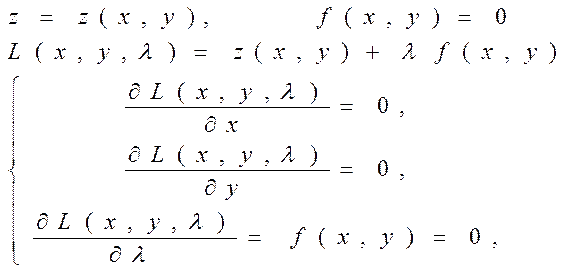
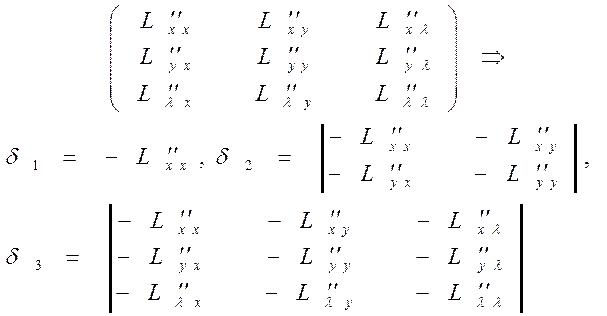
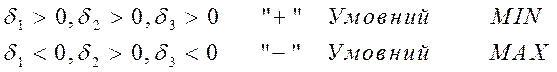
НАЙБІЛЬШЕ ЗНАЧЕННЯ ФУНКЦІЇ 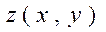В ОБЛАСТІ

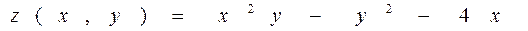
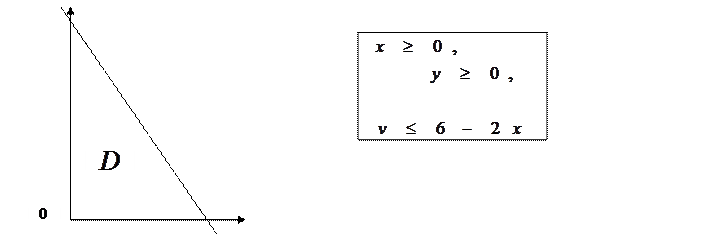
НЕОБХІДНІ УМОВИ:

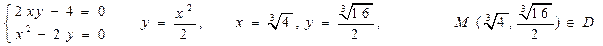
1).

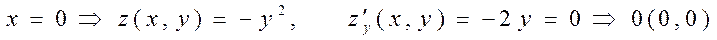
2)

3)

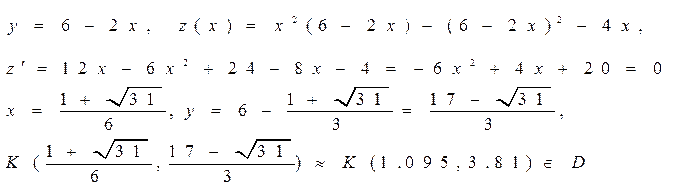
4)

, , ,

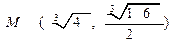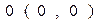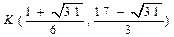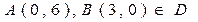
5)

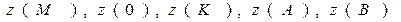
Підставити точки в значення функції та знайти найбільше та наименше її значення