Пример1. Обозначим общее число каналов в групповом сигнале через N.
Обозначим общее число каналов в групповом сигнале через N.
Число каналов в исходной группе – n1.
Число каналов во 2-ой группе, содержащей n1, исходных групп – n2.
Число каналов в 3-ей группе, в которую входят n2 групп, – n3.
Число ступеней преобразований – m.
Тогда общее число каналов  , а число различных фильтров и несущих частот
, а число различных фильтров и несущих частот 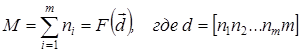 .
.
Для решения задачи нужно найти компоненты вектора d, при которых функция 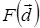 принимает минимальное значение, и выполняются ограничения
принимает минимальное значение, и выполняются ограничения  и
и 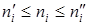 где
где 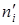 и
и 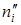 - предельные значения числа каналов в каждой группе.
- предельные значения числа каналов в каждой группе.
Известно, что сумма сомножителей при заданном произведении будет минимальна, если все сомножители одинаковы. n1 = n2 = … = n, тогда N = n∙m,
M = n ∙m.
Подставим значение 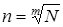 в первое равенство,
в первое равенство, 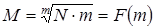 . Для определения минимума находим
. Для определения минимума находим 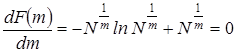 , откуда ln N = m, или ln n = 1, а nopt = e.
, откуда ln N = m, или ln n = 1, а nopt = e.
Таким образом, независимо от общего числа каналов, наименьшее число разнотипного оборудования получим, если выбирать число каналов в группе (n1) близкое к трем и группировать спектры по три ветви в каждом объединении (n2, n3).
Общее количество оборудования, задействованного для формирования группового сигнала 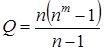 , при n1 = n2 = … = n.
, при n1 = n2 = … = n.
Если несколько отойти от минимума разнотипных устройств, можно значительно сократить общее количество оборудования.
Дата добавления: 2015-08-26; просмотров: 740;
