Тепловые двигатели и холодильные машины. Цикл Карно и его к.п.д. для идеального газа

Из формулировки второго начала термодинамики по Кельвину следует, что вечный двигатель второго вода – периодически действующий двигатель, совершающий работу за счет охлаждения одного источника теплоты, – невозможен.

Для иллюстрации этого положения рассмотрим работу теплового двигателя.

Принцип действия теплового двигателя приведен на рис.8.2.

От термостата с более высокой температурой T₁ называемого нагревателем, за цикл отнимается количество теплоты Q₁, а термостату с более низкой температурой T₂, называемому холодильником, за цикл передается количество теплоты Q₂, при этом совершается работа

А=Q₁–Q₂.

Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине, принцип действия которой представлен на рис.9.3. Системой за цикл от термостата с более низкой температурой Т₂отнимается количество теплоты Q₂ и отдается термостату с более высокой температурой Т₁ количество теплоты Q₁. Для кругового процесса Q=A, но, по условию, Q=Q₂-Q₁<0, поэтому А<0 и Q₂-Q₁= -А, или Q₁=Q₂+A, т. е. количество теплоты Q₁, отданное системой источнику теплоты при более ысокой температуре T₁ больше количества теплоты Q₂, полученного от источника теплоты при более низкой температуре Т₂, на величину работы, совершенной над системой. Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать ее более нагретому. Это утверждение есть не что иное, как второе начало термодинамики в формулировке Клаузиуса.

Основываясь на втором начале термодинамики, Карно вывел теорему: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (Т₁) и холодильников (Т₂) наибольшим к. п. д. обладают обратимые машины; при этом к. п. д. обратимых машин, работающих при одинаковых температурах нагревателей (Т₁) и холодильников (Т₂), равны друг другу и не зависят от природы рабочего тела (тела, совершающего круговой процесс и обменивающегося энергией с другими телами), а определяются только температурами нагревателя и холодильника.

Цикл Карно – наиболее экономичный цикл,состоящий из двух изотерм и двух адиабат. Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ,заключенный в сосуд с подвижным поршнем.

Цикл Карно изображен на рис. 8.4, где изотермические расширение и сжатие заданы соответственно кривыми 1–2 и 3–4, а адиабатические расширение и сжатие – кривыми 2–3 и 4–1.

При изотермическом процессе U= const, поэтому количество теплоты Q₁ полученное газом от нагревателя, равно работе расширения А₁₂, совершаемой газом при переходе из состояния 1 в состояние 2:

A₁₂ =νRT₁ 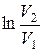=Q₁ (8.13)

При адиабатическом расширении 2-3 теплообмен с окружающей средой отсутствует и работа расширения A₂₃ совершается за счет изменения внутренней энергии A₂₃ =–νC_V(T₂-T₁). Количество теплоты Q₂, отданное газом холодильнику при изотермическом сжатии, равно работе сжатия A₃₄:

A₃₄=νRT₂ 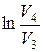=–Q₂. (8.14)

Работа адиабатического сжатия

A₄₁ =–νC_V(T₁–T₂)=–A₂₃.

Работа, совершаемая в результате кругового процесса,

A=A₁₂+ A₂₃+ A₃₄+ A₄₁=Q₁+ A₂₃– Q₂– A₂₃= Q₁– Q₂

определяется площадью, заштрихованной на рис.8.4.

Термический к. п. д. для цикла Карно равен: η = A/Q₁ = (Q₁–Q₂)/Q₁.

Применив уравнение Пуассона для адиабат 2–3 и 4–1, получим

T₁ 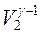= T₂ , .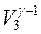

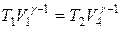Откуда

V₂/V₁ = V₃/V₄. (8.15)

Подставляя (9.13) и (9.14) в формулу (9.2) и учитывая (9.15), получаем

η= 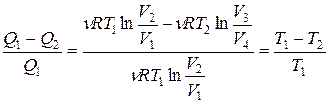, (8.16)

т. е. для цикла Карно к. п. д. действительно определяется только температурами нагревателя и холодильника. Для его повышения необходимо увеличивать разность температур нагревателя и холодильника. Например, при Т₁=400 К и Т₂=300 К η=0,25. Если же температуру нагревателя повысить на 100 К, а температуру холодильника понизить на 50 К, то η=0,5. К. п. д. всякого реального теплового двигателя из-за трения и неизбежных тепловых потерь гораздо меньше вычисленного для цикла Карно.

Обратный цикл Карно положен в основу действия тепловых насосов. В отличие от холодильных машин тепловые насосы должны как можно больше тепловой энергии отдавать горячему телу, например системе отопления. Часть этой энергии отбирается от окружающей среды с более низкой температурой, а часть – получается за счет механической работы, производимой, например, компрессором.

Теорема Карно послужила основанием для установления термодинамической шкалы температур. Сравнив левую и правую части формулы (8.16), получим

Τ₂/T₁=Q₂/Q₁,(8.17)

т. е. для сравнения температур T₁ и T₂ двух тел необходимо осуществить обратимый цикл Карно, в котором одно тело используется в качестве нагревателя, а другое – холодильника. Из равенства (8.17) видно, что отношение температур тел равно отношению отданного в этом цикле количества теплоты к полученному.