Діаграми на сітці Ламберта – Шмідта.

Діаграми цього типу,на відміну від роз-діаграм, характеризують розподіл тріщин за орієнтуванням одночасно в трьох вимірах (по трьох осях), тобто одночасно за кутами та азимутами падіння. Для побудови таких діаграм використовують стереографічні проекції, а якщо точніше – проекції верхньої півкулі на горизонтальну площину (рис. 3.2.6). У даній роботі немає можливості детально зупинитися на розгляді сутності й методології побудови подібних діаграм. Для тих, хто цікавиться цими питаннями докладніше, рекомендуємо звернутися до робіт І.А.Очеретенка, В.В.Трощенка "Стереографические проекции в структурной геологии" (1978) та А.І. Родигіна "Использование азимутальных проекций в структурной геологии" (1973).

Стереографічна проекція є одним із видів перспективного зображення сфери на площині, коли точка зору (центр проектування) розташовується на поверхні сфери, а картинна площина (та, на яку проектується зображення) – у центрі, перпендикулярно до радіуса, який іде до точки зору. Найважливішими особливостями такої проекції є те, що: 1) кола, що лежать на сфері, на картинній площині також проектуються у вигляді кіл, або у вигляді прямої, якщо коло на сфері проходить через центр проекції, 2) кути між дугами, що лежать на сфері, зображуються рівними їм кутами між дугами, спроектованими на картинну площину, тобто кожний кут на сфері проектується на площину без спотворень.

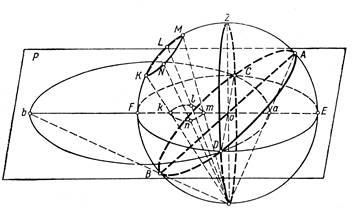
Рис. 3.2.6. Стереографічна проекція точок верхньої півсфери (за І.А.Очеретенком та В.В.Трощенком, 1978)

Стереографічна проекція, як будь-яка інша подібна проекція, зберігає кутові відстані між проектованими прямими або площинами при будь-якій зміні положення картинної площини. Більше того, всередині кола проекції може бути зображена вся півсфера, тобто побудовані проекції практично будь-якої кількості прямих або площин.

Завдяки цим чудовим властивостям стереографічна проекція використовується для розв'язання найрізноманітніших геометричних задач, пов'язаних із визначенням у тримірному просторі кутів між різноманітними напрямками, площинами або тими й іншими. Для цього прямі або площини переносяться паралельно самим собі в одну точку о, біля котрої описується деяким радіусом сфера. Остання з прямими і площинами дає перетинання у вигляді точок і сферичних ліній. Площини, що проходять через центр сфери, дають на її поверхні великі кола, а площини, що проходять поза центром сфери, – малі кола.

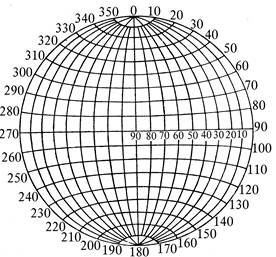
Рис. 3.2.7. Рівноплощинна сітка Ламберта – Шмідта

Сліди перетинання, що перенесені пучками променів та проектуютьсяз центра проектування Z на картинну площину Р, зображуються на ній у вигляді точок, ліній і кругів, тобто дають стереографічні проекції прямих абоплощин. Так, наприклад, напрямок АВзобразиться в стереографічній проекції точкою а.

Площина, що перетинає сферу по великому колу АDВС, проектується на площину Р у вигляді кола аDbС. Але якщо розглядати тільки верхню півсферу, то стереографічною проекцією площини АDВС є дуга CaD, що лежить усередині круга проекції EDFC. З нижньої півсфери та ж площина ADBC проектується на площину Р у вигляді дуги DbC. Стереографічними проекціями більших кіл вертикальних площин ZEZ`F i ZCZ`D є діаметри кола проекції EF та CD. Зображення на картинній площині можна уявити собі як коло нескінченно великого радіуса.

Положення будь-якої точки на сфері визначається за її сферичними координатами (довготою та шириною). При вирішенні геологічних задач на стереографічних моделях роль сферичної довготи виконує азимут падіння (кут між позначеною на сфері нульовою довготою та лінією азимута падіння), а роль сферичної широти – кут між прямою (або площиною) та картинною площиною, котра умовно збігається з горизонтом земної поверхні.

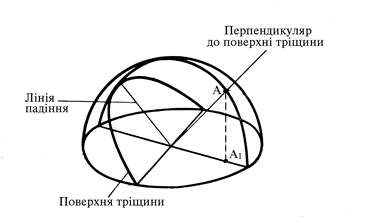
Рис. 3.2.8. Схема, що пояснює положення поверхні тріщини та полюса цієї тріщини на поверхні півкулі (А)

і на горизонтальній проекції цієї півкулі (А₁)

Для зручності й точності побудов стереографічних проекцій прямих та площин, які задаються азимутом та кутом падіння, поверхню сфери розбивають на сітку умовних меридіанів та паралелей. Відбиток подібної сітки на картинну площину називають стереографічною проекцією. Вона являє собою плоский відбиток на картинній площині градусної сітки меридіанів і паралелей верхньої та нижньої півсфер. Існують різноманітні такі проекції. У геології отримали розповсюдження екваторіальна та полярна сітки стереографічної проекції верхньої півсфери. Перша така проекція відома як сітка Вульфа, а друга – як рівноплощинна стереографічна сітка Ламберта – Шмідта (рис. 3.2.7).

У даній роботі розглядаються можливість використання обох типів сіток. Але в цьому розділі ми зупинимося тільки на сітці Ламберта – Шмітда, оскільки вона якнайбільше пристосована до потреб графічного вивчення тріщинної тектоніки.

Стереографічна сітка Ламберта – Шмідта будується шляхом проектування градусної сітки сфери на площину екватора, суміщеної з горизонтальною площиною. При цьому дана сітка побудована таким чином, що рівним площинам на сфері відповідають рівні площини проекцій тих же фігур на картинній площині. Ця сітка дає відносно невеличке порівняно з іншими сітками спотворення лінійного масштабу по площі круга проекції. Зокрема, спотворення градусних поділок на периферичній частині такої сітки складає всього 0,707. Така особливість робить цю сітку дуже зручною для статистично-графічної обробки масових замірів орієнтування площинних елементів структур і в тому числі тріщин.

Техніка побудови стереографічних діаграм тріщинуватості добре описана в роботі Г.Д.Ажгірея "Структурна геологія" (1966). Ця техніка фактично незмінною збереглася і до сьогоднішнього часу. Тому нижче вона подається за викладом цього автора.

При статистичному аналізі тріщинної тектоніки на рівноплощинну сітку замість площин тріщин, що автоматично зображувалися б на сітці у формі ліній великих кіл і було б надзвичайно громіздко, виносять тільки полюси цих площин – проекції точок перетинання з верхньою півсферою нормалей до площин тріщин (рис. 3.2.8). Таким чином, кожна тріщина зобразиться на діаграмі точкою.

Для зручності діаграму будують на листі кальки, який накладається на сітку, що служить трафаретом. При цьому на кальці викреслюється коло, що відповідає зовнішньому колу сітки-трафарету, а на колі рискою позначається місце нуля, котре одночасно є орієнтуванням діаграми, що вказує напрямок півночі. Паперова калька в центрі зміцнюється невеличким шматочком прозорої стрічки і наколюється на центр трафарету, який забезпечує обертання кальки.

При виконанні даної операції враховують ту обставину, що точки, які падають безпосередньо на лінію зовнішнього кола, тобто є відповідними вертикальним тріщинам, можуть із рівним правом бути нанесені як на один бік великого кола, так і на його протилежний бік (тому що у вертикальній тріщині, яка простягається, наприклад, широтно, є два азимути падіння – на північ, тобто 0° під кутом 90°, і таким же підставою на південь, тобто 180° під кутом 90°). Проте завдається тільки одна точка (будь-яка з двох).

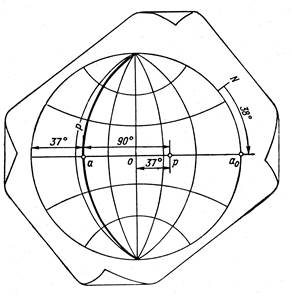
Рис.3.2.9. Побудова проекції та полюса тріщини