Топология физических связей

В первую очередь необходимо выбрать способ организации физических связей, то есть топологию. Под топологией вычислительной сети понимается конфигурация графа, вершинам которого соответствуют компьютеры сети (иногда и другое оборудование, например концентраторы), а ребрам - физические связи между ними. Компьютеры, подключенные к сети, часто называют станциями или узлами сети.

Заметим, что конфигурация физических связейопределяется электрическими соединениями компьютеров между собой и может отличаться от конфигурации логических связей между узлами сети. Логические связи представляют собой маршруты передачи данных между узлами сети и образуются путем соответствующей настройки коммуникационного оборудования.

Выбор топологии электрических связей существенно влияет на многие характеристики сети. Например, наличие резервных связей повышает надежность сети и делает возможным балансирование загрузки отдельных каналов. Простота присоединения новых узлов, свойственная некоторым топологиям, делает сеть легко расширяемой. Экономические соображения часто приводят к выбору топологий, для которых характерна минимальная суммарная длина линий связи.

Рассмотрим некоторые, наиболее часто встречающиеся топологии.
Полносвязная топология (рис. 1.10, а) соответствует сети, в которой каждый компьютер сети связан со всеми остальными. Несмотря на логическую простоту, этот вариант оказывается громоздким и неэффективным. Действительно, каждый компьютер в сети должен иметь большое количество коммуникационных портов, достаточное для связи с каждым из остальных компьютеров сети.

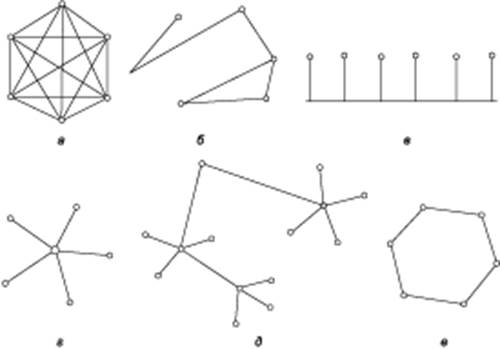
Рис. 1.10. Типовые топологии сетей

Для каждой пары компьютеров должна быть выделена отдельная электрическая линия связи. Полносвязные топологии применяются редко, так как не удовлетворяют ни одному из приведенных выше требований. Чаще этот вид топологии используется в многомашинных комплексах или глобальных сетях при небольшом количестве компьютеров.
Все другие варианты основаны на неполносвязных топологиях, когда для обмена данными между двумя компьютерами может потребоваться промежуточная передача данных через другие узлы сети.
Ячеистая топология (mesh) получается из полносвязной путем удаления некоторых возможных связей (рис. 1.10, б). В сети с ячеистой топологией непосредственно связываются только те компьютеры, между которыми происходит интенсивный обмен данными, а для обмена данными между компьютерами, не соединенными прямыми связями, используются транзитные передачи через промежуточные узлы. Ячеистая топология допускает соединение большого количества компьютеров и характерна, как правило, для глобальных сетей.

Общая шина(рис. 1.10, в) является очень распространенной (а до недавнего времени самой распространенной) топологией для локальных сетей. В этом случае компьютеры подключаются к одному коаксиальному кабелю по схеме "монтажного ИЛИ". Передаваемая информация может распространяться в обе стороны. Применение общей шины снижает стоимость проводки, унифицирует подключение различных модулей, обеспечивает возможность почти мгновенного широковещательного обращения ко всем станциям сети. Таким образом, основными преимуществами такой схемы являются дешевизна и простота разводки кабеля по помещениям. Самый серьезный недостаток общей шины заключается в ее низкой надежности: любой дефект кабеля или какого-нибудь из многочисленных разъемов полностью парализует всю сеть. К сожалению, дефект коаксиального разъема редкостью не является. Другим недостатком общей шины является ее невысокая производительность, так как при таком способе подключения в каждый момент времени только один компьютер может передавать данные в сеть. Поэтому пропускная способность канала связи всегда делится здесь между всеми узлами сети.
Топология звезда (рис. 1.10, г). В этом случае каждый компьютер подключается отдельным кабелем к общему устройству, называемому концентратором, который находится в центре сети. В функции концентратора входит направление передаваемой компьютером информации одному или всем остальным компьютерам сети. Главное преимущество этой топологии перед общей шиной - существенно большая надежность. Любые неприятности с кабелем касаются лишь того компьютера, к которому этот кабель присоединен, и только неисправность концентратора может вывести из строя всю сеть. Кроме того, концентратор может играть роль интеллектуального фильтра информации, поступающей от узлов в сеть, и при необходимости блокировать запрещенные администратором передачи.
К недостаткам топологии типа звезда относится более высокая стоимость сетевого оборудования из-за необходимости приобретения концентратора. Кроме того, возможности по наращиванию количества узлов в сети ограничиваются количеством портов концентратора. Иногда имеет смысл строить сеть с использованием нескольких концентраторов, иерархически соединенных между собой связями типа звезда (рис. 1.10, д). В настоящее время иерархическая звезда является самым распространенным типом топологии связей как в локальных, так и глобальных сетях.
В сетях с кольцевой конфигурацией (рис. 1.10, е) данные передаются по кольцу от одного компьютера к другому, как правило, в одном направлении. Если компьютер распознает данные как "свои", то он копирует их себе во внутренний буфер. В сети с кольцевой топологией необходимо принимать специальные меры, чтобы в случае выхода из строя или отключения какой-либо станции не прервался канал связи между остальными станциями. Кольцо представляет собой очень удобную конфигурацию для организации обратной связи - данные, сделав полный оборот, возвращаются к узлу-источнику. Поэтому этот узел может контролировать процесс доставки данных адресату. Часто это свойство кольца используется для тестирования связности сети и поиска узла, работающего некорректно. Для этого в сеть посылаются специальные тестовые сообщения.

В то время как небольшие сети, как правило, имеют типовую топологию - звезда, кольцо или общая шина, для крупных сетей характерно наличие произвольных связей между компьютерами. В таких сетях можно выделить отдельные произвольно связанные фрагменты (подсети), имеющие типовую топологию, поэтому их называют сетями со смешанной топологией(рис. 1.11).

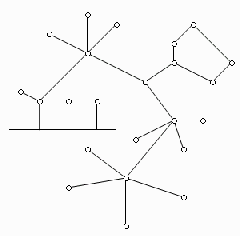
Рис. 1.11. Смешанная топология