Гидродинамические расчеты фильтрации аномальных нефтей.

Рассматривается установившаяся фильтрация аномальной нефти в однородном круговом пласте мощностью h, проницаемостью К. Радиус контура питания обозначен через R_к, а радиус скважины – через r_с. На контуре питания поддерживается давление, равное Р_{к, а} на забое скважины – Р_с. В соответствии со схематизацией фильтрации, приведенной выше, круговой пласт делится на три зоны с внешними радиусами соответственно r_m, r_g и R_к. Давления на границе первой и второй зоны обозначены через Р_m, а на границе второй и третьей зон – Р_g.

В первой зоне вязкость нефти равна μ_m, в третьей – μ₀, а во второй зоне изменяется в зависимости от градиента по закону

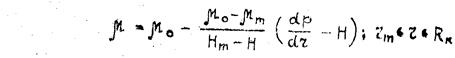(36)

где р, r – соответственно переменное давление и координата точки, в которой определено давление.

Внешние границы первой и второй зон при известных значениях μ_m, μ₀, Н, Н_к, К зависят от дебита Q и определяются по формулам

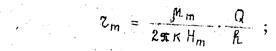(37)

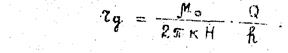(38)

Как видно из приведенной формулы (37), значение радиуса первой зоны прямо пропорционально вязкости нефти μ_m, удельному дебиту скважины (Q/h) и обратно пропорционально произведению коэффициента проницаемости на градиент давления предельного разрушения структуры в нефти. При прочих равных условиях, чем больше вязкость нефти, тем дальше от скважины располагается зона проявления аномальных свойств нефти. В низкопроницаемых пластах радиус первой зоны больше, чем в высокопроницаемых. Однако следует отметить, что с уменьшением проницаемости существенно возрастают граничные градиенты давления. Аналогично изменяется и радиус второй зоны в зависимости от параметров, входящих в формулу (38).

При проведении расчетов по формулам (37) и (38) следует придерживаться следующих размерностей величин: μ_m и μ₀, сП; Q, см³/с; К, Д; Н и Н_m, кгс/(см²∙м); h, см. Выпишем формулы для расхода жидкости через параметры всех трех зон:

1-ая зона 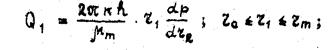(39)

2-ая зона 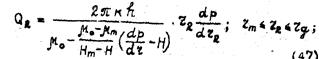(40)

3-я зона 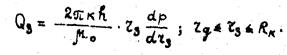(41)

Из условия неразрывности потока получим равенство

Q₁ = Q₂ = Q₃ = Q (42)

Подставив значения расходов, после некоторых упрощений имеем

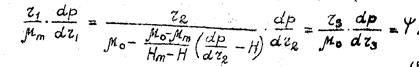(43)

Постоянное ψ определяется по формуле

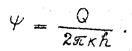(44)

Для получения зависимости дебита скважины от депрессии на пласт воспользуемся следующим очевидным равенством

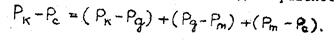(45)

Второе слагаемое равенства (45) вычисляется по формуле

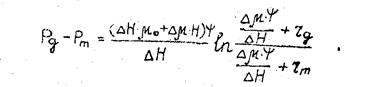(46)

Значение давления в любой точке во второй зоне кругового пласта вычисляется по зависимости

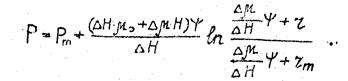(47)

В равенствах (46) и (47) для удобства записей введены следующие дополнительные обозначения: ∆ Н = Н_m – Н; ∆μ = μ₀ – μ_m.

Значение давления в первой и третьей зонах вычисляется по формуле Дюпюи подстановкой в нее параметров соответствующих зон.

Давления на границах зон определяются из формул

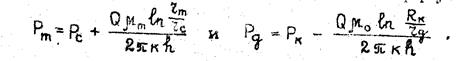(48)

Подставляя (48) в равенство (45), получим формулу для расчета дебита скважины в виде

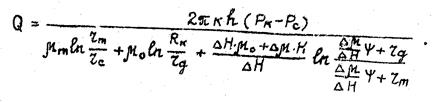(49)

В полученной формуле (49) для расчета дебита скважины, работающей в круговом пласте, внешние радиусы зон r_m и r_g зависят от дебита скважины. Поэтому при расчетах необходимо задаваться дебитом и находить разность пластового и забойного давлений. Для решения практических задач эксплуатации скважин следует построить график зависимости Q от Р_к-Р_с. Тогда, имея такой график, представляется возможным находить любой из параметров Q, Р_к, Р_с, характеризующих режим работы скважины.

Пример расчета:

Исходные данные: µ₀ = 200 сП; μ_m = 30 сП; Н = 0,0002 кгс/см²∙см;

Н_m = 0,0008 кгс/см²∙см; К = 0,2 Д; R_к = 20000 см; r_с = 10 см.

Расчет ведется по формуле (49).

1. Вычисляем значения комплекса постоянных для расчета

2. Определяем значение постоянного перед логарифмом третьего слагаемого знаменателя формулы (49)

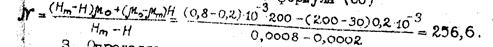
3. Определяем значения параметра

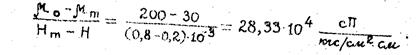
4. Задаемся удельным дебитом скважины

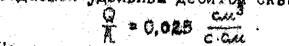
5. Находим значение параметра

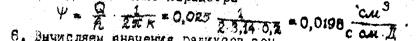
6. Вычисляем значения радиусов зон

r_m = 30000∙(Q/h) = 30000∙0,025 = 750 см;

r_g = 79620∙0,025 = 19905 см;

7. Находим значения первого и второго слагаемых знаменателя

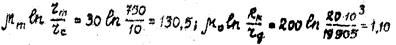
8. Вычисляем значение выражения под логарифмом третьего слагаемого. Прологарифмируем и умножим на N:

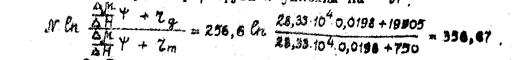
9. Подставляя полученные значения слагаемых и решая равенство относительно (Р_к-Р_с), находим

Р_к-Р_с = 9,66 кгс/см²

Для получения полного графика зависимости Q = ƒ(Р_к-Р_с) необходимо задаваться несколькими значениями удельных дебитов скважины до тех пор, пока не достигнет граница первой зоны контура питания. В дальнейшем задачи решаются с использованием полученного графика.

Как было отмечено выше, одновременное существование всех трех характерных зон в пласте возможно только при соответствующих сочетаниях параметров или при очень малых расходах нефти. Поэтому, если потребуется график изменения дебита в широком интервале изменения депрессии на пласт, то одной формулы (49) недостаточно, а нужно иметь еще одну расчетную формулу, полученную из условия существования двух зон – первой и второй.

При пуске скважины существуют все три зоны, и в течение некоторог времени внешние границы зон перемещаются к контуру питания до тех пор, пока процесс фильтрации не станет стационарным.

Если дебит скважины значительный, то граница второй зоны достигает контура питания. В результате этого вся область дренажа будет разделена на две зоны.

Расчетную формулу для дебита скважины в случае «двухзонной» фильтрации можно получить путем аналогичных рассуждений.

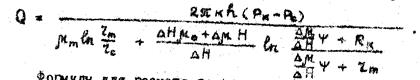(50)

Формулы для расчета распределения давления в пласте, дебита скважины, забойного и контурного давления для случая 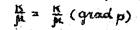при необходимости можно получить, используя приведенную выше схему решения задачи.