Парамагнетизм.

Парамагнетиками являются вещества, атомы (или молекулы) которых обладают собственными, отличными от нуля, орбитальными моментами. При 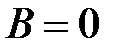все магнитные моменты ориентированы хаотически, и 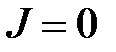. Энергия магнитного момента во внешнем магнитном поле (рис.4.11):

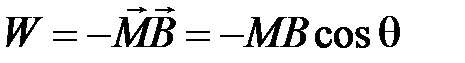. (4.59)

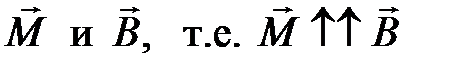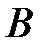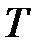Минимум энергии отвечает случаю сонаправленных коллинеарных векторов , благодаря чему при включении поля магнитные моменты атомов стараются ориентироваться по полю. Этому препятствует тепловая энергия. В результате устанавливается некоторое равновесие, определяющее величину намагниченности при данных значениях и . Для расчета восприимчивости парамагнетика рассмотрим модель идеального газа магнитных стрелок с магнитным моментом .

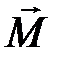Для этого необходимо учесть, что среднее значение магнитного момента атома с учетом распределения Больцмана определяется так. Число моментов в телесном угле :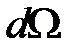

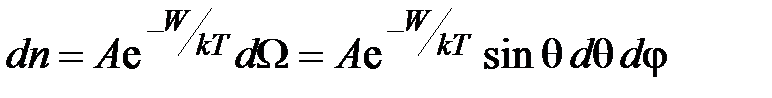. (4.60)

В общем случае выражение для среднего значения проекции магнитного момента на ось Z имеет вид

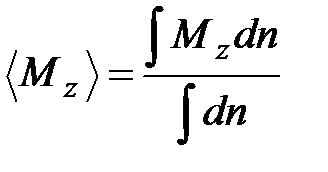
или:

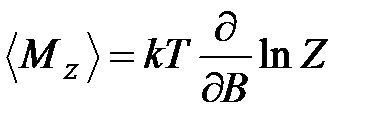, (4.61)

где 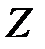представляет собой статинтеграл:

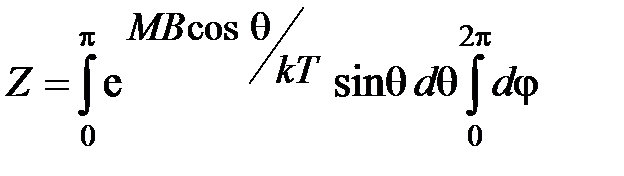. (4.62)

Используя следующее соотношение: 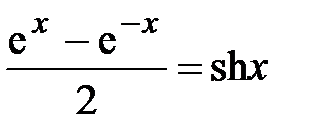, получаем:

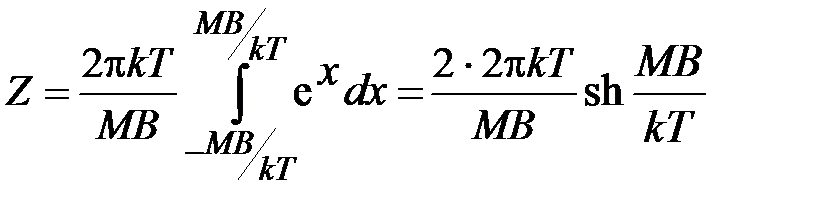. (4.63)

Тогда (4.61) перепишется таким образом:

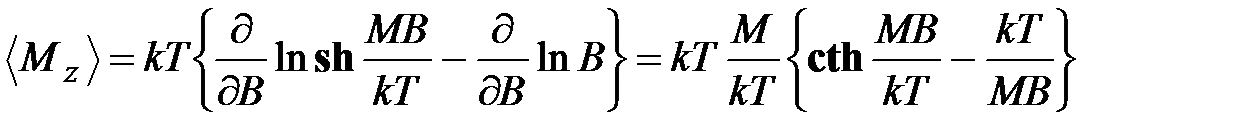. (4.64)

Иначе:

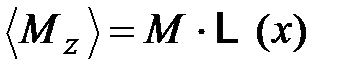
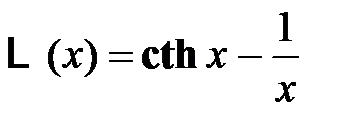, (4.65)

где 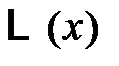- функция Ланжевена. Тогда магнитный момент единицы объема вещества:

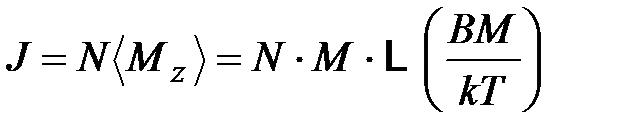. (4.66)

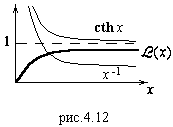
Зависимость 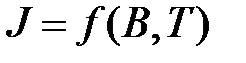определяется функцией Ланжевена, представленной на рис.4.12. Рассмотрим предельные случаи больших и малых магнитных полей.

1. 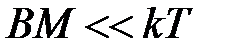‑ слабые поля.

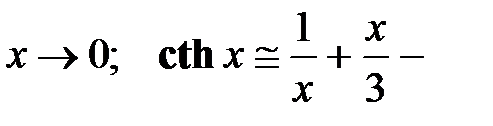
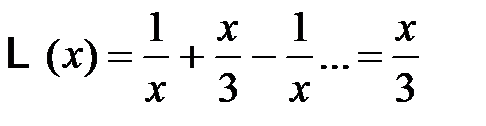
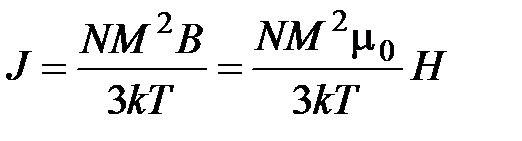. (4.67)

Было использовано, что 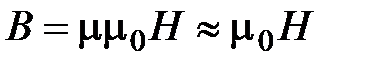при 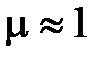. Из сравнения (4.19) и (4.67) видно, что:

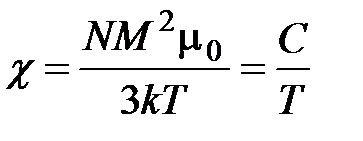. (4.68)

Формула представляет зависимость 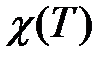и носит название закона Кюри. Здесь 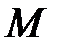- магнитный момент атома; 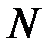- число атомов в единице объема, C - постоянная Кюри.

2. 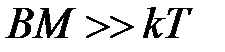‑ сильные поля.

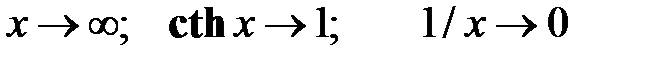
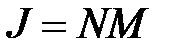, (4.69)

т.е. все магнитные моменты выстраиваются параллельно.

Почему рассматриваемая модель получила название идеального газа магнитных стрелок? Потому что в этой модели не учитывается взаимодействие магнитных моментов.

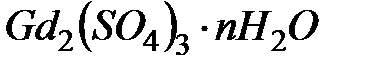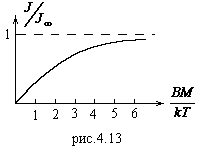
Поэтому экспериментальная проверка теории Ланжевена лучше всего может быть проведена на газах и солях редкоземельных металлов, например, , где ионы 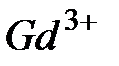в кристаллической решетке далеки друг от друга и их магнитные моменты не взаимодействуют. На рис.4.13 представлена зависимость 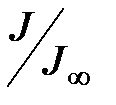от величины 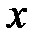. Видно, что насыщение достигается при 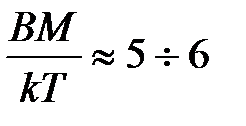. Можно оценить величину 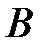, получающуюся при этом. Для .

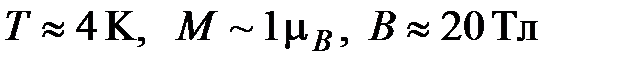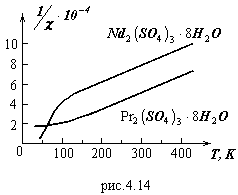
При изучении 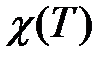в слабых полях должен выполняться закон Кюри. При низких температурах проявляется взаимодействие магнитных моментов, что ведет к отклонению от закона Кюри. Это хорошо видно из графиков температурной зависимости величины, обратной восприимчивости, показанных на рис.4.14.