Процессы, протекающие в цилиндре с реальным хладагентом. Процесс расширения.

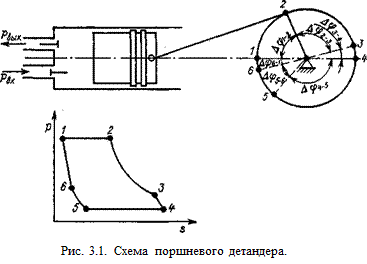Рассмотрим процесс расширения 2–3. В этом процессе масса газа практически остается постоянной (если допустить, что утечка мала); теплообмен имеет знакопеременный характер: в начальной стадии процесса тепловой поток направлен от газа к стенке, а в конце процесса он меняет направление и теплота отводится к газу от более теплой стенки.

В идеальном детандере этот процесс может быть аппроксимирован изоэнтропой, в реальном детандере – политропой. При определении термодинамических параметров хладагента в конце процесса расширения следует исходить из условия постоянства массы в этом процессе:

.

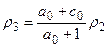В изоэнтропном процессе расширения s₃=s₂ и все термодинамические параметры могут быть определены по известным ρ₃ и s₃: Т₃=Т(ρ₃, s₃); р₃=p(ρ₃, s₃) и т.д.

Реальный процесс расширения может быть аппроксимирован политропой конечных параметров, проходящих через точки 2 и 3. Под политропным понимается такой процесс, в котором подвод теплоты пропорционален разности температур

.

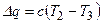Коэффициент пропорциональности с в этом уравнении называется теплоемкостью политропного процесса, которая в этом процессе остается постоянной.

В процессе 2–3 теплообмен имеет знакопеременный характер, поэтому, при допущении о линейном характере изменения температуры в этом процессе получаем

,

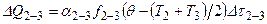где α_2–3 – коэффициент теплообмена процесса 2–3; 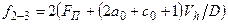– средняя площадь поверхности теплообмена в этом процессе; 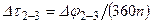– время процесса расширения.

Таким образом, последовательность определения параметров в процессе расширения такова: приняв произвольное значение η_Т=1, что соответствует изоэнтропному процессу, находим термодинамические параметры в точке 3 в нулевом приближении. Оцениваем тепловой поток ∆Q_2–3 и определяем политропный КПД:

,

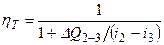после чего снова определяем параметры в точке 3 и ρ₃ при уточненном значении политропного КПД.

Для идеального газа параметры в политропном процессе могут быть определены по формуле

,

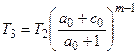где m – показатель политропы конечных параметров.