Уравнение сохранения энергии для ТД.

Общее уравнение энергии. Уравнение энергии может быть записано в тепловой форме (через энтальпию газа) и в механической форме (через давление газа).

Уравнение энергии в тепловой форме для потока массы газа 1 кг/с между двумя произвольными сечениями I и II в условиях обмена работой и теплотой с окружающей средой имеет вид:

в дифференциальной форме ;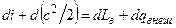

в интегральной форме ,

где L_в – внешняя работа, подведенная через вал; q_внеш – внешняя теплота, подведенная на участке I–II; 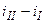и –·и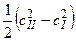зменения энтальпии и кинетической энергии потока массы газа.

Для ТД и его элементов в условиях подвода тепла уравнение имеет вид:

,

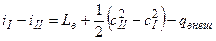или через энтальпию заторможенного потока .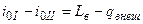

Уравнение энергии в механической форме от p_I до p_II имеет вид:

.

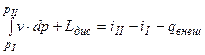При подводе внешней теплоты в ТД q_внеш>0.

Представляют интерес уравнения, получающиеся при сравнении уравнений энергии в тепловой и в механической формах. Для турбомашин любого типа получаем следующее общее уравнение:

.

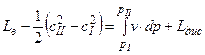Это обобщенное уравнение Бернулли удобно тем, что связывает внешнюю работу с политропной работой и диссипированной энергией; внешний теплообмен не отражается в этом уравнении.

Применительно к расширительной машине оно примет вид:

.

Физический смысл полученного уравнения заключается в следующем: в расширительной машине политропная работа расширения потока массы газа равна сумме внешней работы, диссипированной энергии и изменения кинетической энергии.

Рассмотренные уравнения можно применять к одноступенчатым и многоступенчатым расширительным машинам, а также к отдельным их элементам.