Консервативные силы. Силы, работа которых не зависит от пути, по которому двигалась частица, а зависит лишь от начального и конечного положений частицы

Легко показать, что работа сил на любом замкнутом пути равна нулю. Разобьем произвольный замкнутый путь (рис.1) точками 1 и 2 (взятыми также произвольно) на два участка, обозначенных римскими цифрами I и II. Работа на замкнутом пути слагается из работ, совершаемых на этих участках:

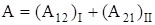(8)

Рис.1

Изменение направления движения по участку II на обратное сопровождается заменой всех элементарных перемещений ds на - ds, вследствие чего 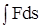изменяет знак на обратный. Отсюда заключаем, что 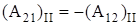. Произведя замену в (8), получим, что

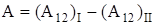
Вследствие независимости работы от пути последнее выражение равно нулю. Таким образом, консервативные силы можно определить как силы, работа которых на любом замкнутом пути равна нулю.