Диполь Герца
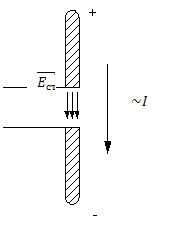
Диполь Герца физически может быть представлен в виде вибратора, состоящего из двух проводников, на концах которого расположены переменные во времени заряды.
Рис. 18.2. Диполь Герца
Ток 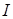 замыкается в промежутке между проводниками током смещения
замыкается в промежутке между проводниками током смещения 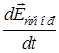 , создаваемым переменным сторонним полем, образующимся за счет подключения проводников к Э.Д.С. стороннего источника.
, создаваемым переменным сторонним полем, образующимся за счет подключения проводников к Э.Д.С. стороннего источника.
Для диполя Герца как линейного проводника длиной l векторный запаздывющий потенциал
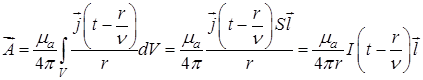 . (18.1)
. (18.1)
Вектора Герца
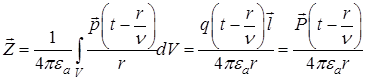 , (18.2)
, (18.2)
где величину
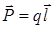 (18.3)
(18.3)
– называют дипольным моментом.
Для гармонических волн:
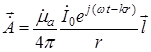 . (18.4)
. (18.4)
Зная 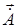 можно найти
можно найти 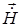 т.к.
т.к.
 . (18.5)
. (18.5)
Зная 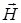 из первого уравнения Максвелла (в сводном пространстве вне диполя) можно найти
из первого уравнения Максвелла (в сводном пространстве вне диполя) можно найти 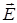
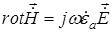 , (18.7)
, (18.7)
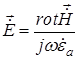 . (18.8)
. (18.8)
Для упрощения вычислений поместим центр диполя в начало координат, а диполь ориентируем вдоль оси z, рис. 18.3.
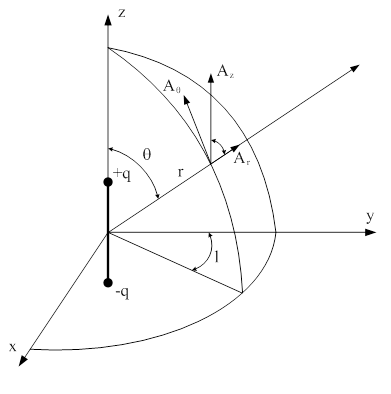
Рис. 18.3. Векторный потенциал диполя Герца
В этом случае имеем лишь одну проекцию  на ось z в декартовой системе координат
на ось z в декартовой системе координат
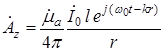 . (18.9)
. (18.9)
В сферической системе координат
 ,
,  ,
, 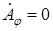 .
.
В силу сферической симметрии
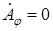 И
И 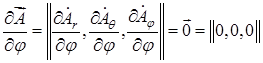 . (18.10)
. (18.10)
Записывая выражения для операции ротора в сферической системе координат
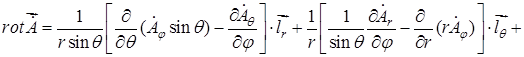
 , (18.11)
, (18.11)
и учитывая (18.10), находим, что единственная проекция  ,(
,( 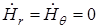 ) равна
) равна
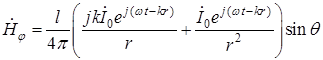 . (18.12)
. (18.12)
Левую и правую части этого равенства можно сократить на временной множитель 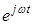 , оставив лишь пространственную часть. Умножив и разделив правую часть на
, оставив лишь пространственную часть. Умножив и разделив правую часть на 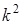 , получим:
, получим:
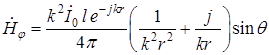 ,
, 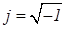 . (18.13)
. (18.13)
Электрический вектор
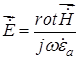 ,
,
очевидно, перпендикулярен 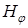 и имеет лишь две компоненты
и имеет лишь две компоненты
 ,
, 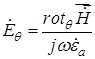 . (18.14)
. (18.14)
Заменяя в формуле (18.11) для ротора вектора вектор 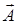 на вектор
на вектор 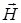 , получим:
, получим:
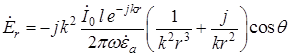 , (18.15)
, (18.15)
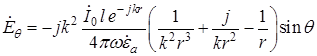 . (18.16)
. (18.16)
Т.к. 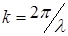 , то формулы (18.13, 18.14) целесообразно записать в виде:
, то формулы (18.13, 18.14) целесообразно записать в виде:
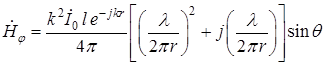 , (18.17)
, (18.17)
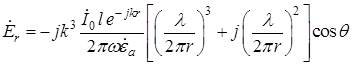 , (18.18)
, (18.18)
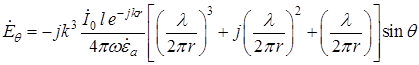 . (18.19)
. (18.19)
Дата добавления: 2015-05-13; просмотров: 1105;
