Чаще при расчетах пользуются размерностью г/кг с.в.
Относительная влажность (%) определяется как отношение парциальных давлений водяного пара в ненасыщенном и насыщенном состоянии:
j = Рп / Рн.п. (2.9.)
Учитывая данное соотношение, выражение для влагосодержания можно представить в виде:
d = 0.623 j Рнп / (Рб - j Рнп) (2.10.)
Энтальпия влажного воздуха определяется:
i = i с.в. + i п , кДж/кг (2.11.)
i с.в. = Ср t =1.005 t
i п = (r + Cp п t) d/1000 = (2500 +1.8 t) d/1000
i = 1.005 t + (2500 +1.8 t ) d/1000 (2.12.)
где r – теплота фазового перехода.
2.4.2. i – d диаграмма влажного воздуха
i – d диаграмма влажного воздуха устанавливает связь между основными параметрами воздуха – t, i, d, j, Рп. Впервые была предложена Л.К. Рамзиным (первый директор Всесоюзного теплотехнического института) в 1918г. (рис.2.7.).
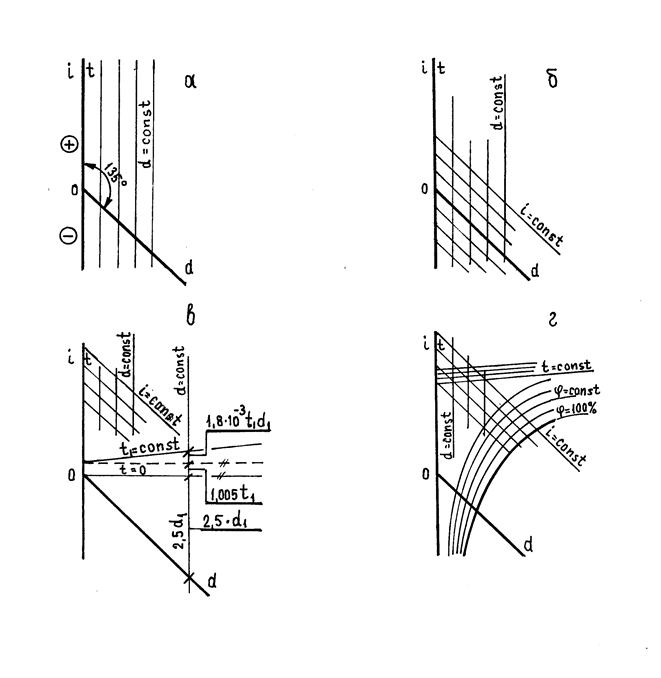
Рис.2.7
Построение i-d диаграммы
Диаграмма построена на основе уравнений (2.10.) и (2.12.) в косоугольной системе координат. Угол между осями координат i и d составляет обычно135о, что позволяет расширить рабочую область на поле диаграммы (рис.2.7.а). Значения влагосодержания отложены на оси абсцисс, энтальпии – на оси ординат, также на оси ординат ( или параллельно основной оси ординат) указаны значения температуры. Значения энтальпии и температуры могут быть положительными и отрицательными. Линии постоянного влагосодержания d=const параллельны оси ординат, соответственно линии i=const параллельны оси абсцисс(рис.2.7.а,б.).
Для определения положения изотерм на диаграмме (рис.2.7.в) необходимо проанализировать уравнение (2.12.). При построении изотермы t=0 уравнение (2.12) имеет вид:
i = 2500 d /1000 =2.5 d
При d=10 г/кг с.в.® i = 25 d
Уравнение (2.12.) для изотермы t1=10°С имеет следующий вид:
i=10.05 + 2500 d/1000 + 18 d/1000
при d=0 г/кг с.в.® i = 10.05
при d=10 г/кг с.в.® i=10.05 + 25+ 0.18 =35.68
Таким образом, можно сделать вывод о непараллельности изотерм на i – d диаграмме.
На рис.2.7.г. кроме вышеуказанных линий нанесены линии постоянных значений относительной влажности воздуха j=const. Для их построения прежде всего строится кривая, соответствующая состоянию полного насыщения воздуха водяным паром j=100%. Зависимость давления водяного пара в насыщенном состоянии от температуры определена экспериментально и приведена в специальных таблицах термодинамического состояния влажного воздуха, составленных М.П.Вукаловичем. Пользуясь этими таблицами и формулой (2.8.), можно найти на i-d диаграмме положение точек, соответствующих состоянию полного насыщения воздуха водяными парами. Геометрическое место этих точек дает положение кривой j=100%. Зависимость (2.10) позволяет определить относительно j=100% положение остальных линий j=const, соответствующим другим значениям относительной влажности воздуха. Положение этих кривых зависит от величины барометрического давления. При построениях необходимо использовать диаграммы для соответствующего среднего барометрического давления местности. При изменении барометрического давления отношение j/ Рб остается постоянным. Это положение позволяет использовать i-d диаграмму, построенную для одного давления, при другом барометрическом давлении.
В нижней части i-d диаграммы на рис.2.8. проведена кривая парциального давления во-
дяного пара, имеющая самостоятельную ось ординат. Она связывает в соответствии с выраже-
нием (2.8) влагосодержание d с парциальным давлением водяного пара Рп :
Рп = d Рб/ (0.623 + d )
Ось ординат этого графика является шкалой парциального давления водяного пара. Значение Рп определяется по линии d=const.
Любая точка на i – d диаграмме соответствует определенному тепловлажностному состоянию воздуха. При 2-х известных параметрах (кроме значений d и Рп) можно определить все остальные (рис.2.8.). Например, известны значения t А и i А, по которым определяется положение точки А на i – d диаграмме, а затем находится значение d А , j А и РпА.
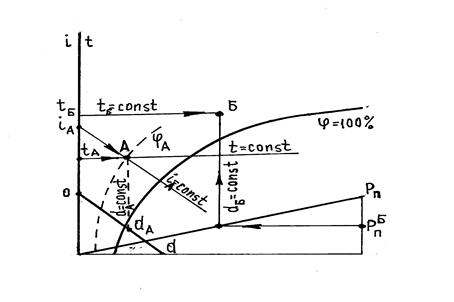 |
Рис.2.8.
В расчетах вентиляции и СКВ часто используют понятия температуры точки росы ( tр) и температуры мокрого термометра ( tм ). Эти параметры соответствуют состоянию полного насыщения воздуха водяным паром (j=100%) при условии d=const (tр.) и i=const (tмт ). Построение приведено на рис.2.9, 2.10.
Температура мокрого термометра - это та минимальная температура, до которой можно охладить воздух до полного его насыщения водяным паром при условии i=const (tмт ).
Температура точки росы - это та минимальная температура, до которой можно охладить воздух до полного его насыщения водяным паром при условии d=const (tр.)
2.4.3.Изображение на i – d диаграмме процессов изменения тепловлажностного состояния воздуха
В вентиляционном процессе в общем случае происходит изменение всех параметров, в частности i и d . На рис. 2.10. показана прямая линия Н-К, характеризующая процесс изменения параметров, например, от точки Н до точки К. При этом величина энтальпии изменилась на величину Di, а величина влагосодержания - на величинуD d. Если расход воздуха, участвующий в процессе обозначим G, кг/с, то количество теплоты переданное воздуху (отданное воздухом) в процессе, можно определить:
Q = G( iк – i н ), кДж /с (2.13.)
Соответственно, количество влаги, определяется из выражения:
GW= G(d к – d н ), кг/с (2.14.)
Рис.2.9
Определение температуры мокрого термометра
Разделим выражение (2.13.) на (2.14.):
Q/GW =( iк – i н )/(d к – d н )=Di /Dd = e, кДж / кг (2.15.)
Это отношение определяет угол наклона к оси абсцисс прямой, изображающей процесс. Прямая называется лучом процесса, а величину e - угловым коэффициентом луча процесса.
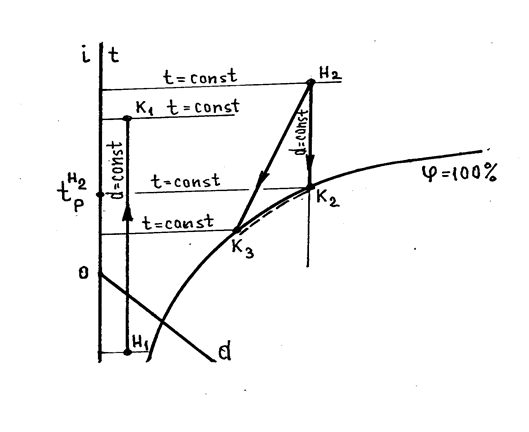 |
Рис.2.10
Дата добавления: 2015-05-08; просмотров: 1884;
