При этом нужно помнить, что
а) фаза определяется длиной пути r , пройденного волнами,
б) амплитуда колебаний, приходящих в точку Р, зависит от размеров площади DS , занятой элементарными источниками, расстояния r и угла a между нормалью к поверхности DS и направлением r.
Для упрощения подсчетов Френель ввел метод зон.
Зона Френеля – участок волнового фронта, выбранный таким образом, что разность хода от двух соседних зон до одной и той же точки экрана отличается на l/2.
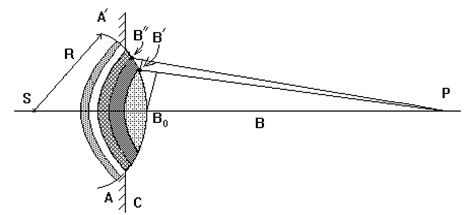
Рис. 2
Пусть свет от точечного источника S проходит через круглое отверстие (диафрагму) в непрозрачном экране (рис. 2). Так как волновой фронт точечного источника по форме представляет собою сферу, то в диафрагме укладывается участок сферического волнового фронта - шаровой сегмент AA¢. Разобьем его на сферические кольца такой ширины, чтобы расстояния от сходственных точек B¢ и B² соседних колец до точки P на экране удовлетворяли условию:
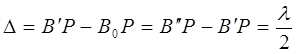 .
.
Такой выбор ширины колец приведет к тому, что колебания, приходящие от соседних зон в точку Р, окажутся в противофазе. Вычислим результирующую амплитуду колебаний в точке Р. Для этого определим величину площади одной из зон Френеля (рис. 3). Эту величину DS найдем как разность площадей к и (к - 1) сферических колец:
DS = Sк - Sк-1. (1)
где 
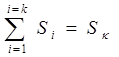 ,
, 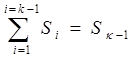 .
.

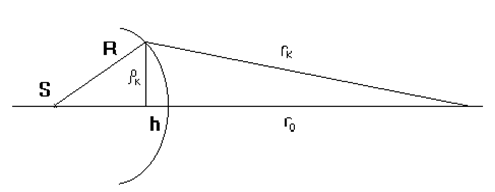
Рис. 3
Поверхность шарового сегмента выразим как сумму площадей всех к зон Френеля, начиная с первой:
Sк = 2 p Rh , (2)
Найдем выражение для h, где h – высота шарового сегмента, направленности которого укладывается к зон Френеля.
Из рис.3 видно, что
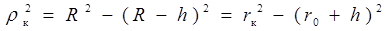 ,
,
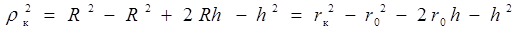 ,
,
откуда считая h2®0,
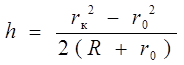 ,
,
но 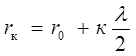 , тогда
, тогда 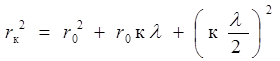 ;
;
при 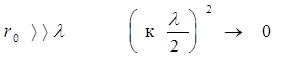 , тогда
, тогда 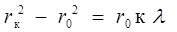 ,
,
откуда
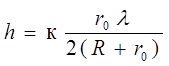 . (3)
. (3)
Подставляя (3) в (2), получим 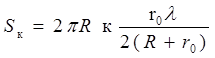 .
.
Используя выражение (1), выразим площадь одной зоны Френеля:
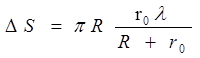 . (4)
. (4)
Как видно, площадь каждой зоны не зависит от номера зоны, следовательно, площади всех зон приблизительно равны. Это можно было предположить без вывода, так как количество вторичных источников, размещенных в каждой зоне Френеля и посылающих свет в точку Р, должно быть одинаково, иначе результат сложения волн в точке Р не будет предсказуем. Таким образом, от величины DS результирующая амплитуда не зависит. Амплитуда будет зависеть от расстояния r, пройденного волной от каждой зоны, причем, чем больше номер зоны, тем больше r. Кроме того, с ростом номера зоны растет и угол a. Освещенность экрана определяется углом падения света на экран:
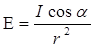 .
.
Угол a (рис.1) - угол падения света на экран.
Исходя из вышесказанного, можно утверждать, что амплитуда колебаний с увеличением номера зоны будет монотонно убывать
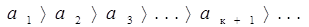
При сложении колебаний от двух соседних зон нужно учитывать, что в точку Р эти колебания приходят в противофазе, поэтому
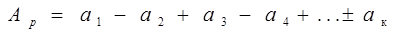 ,
,
где знак (+) для к – нечетного номера зоны,
знак (-) для к – четного.
Разобьем амплитуды нечетных зон на два слагаемых
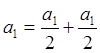 ,
,
тогда при к – нечетном имеем:
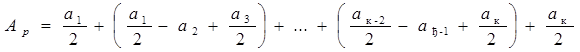 ;
;
при к – четном имеем:
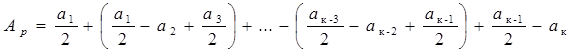 .
.
Учитывая, что a к-1 > a к > a к+1 , введем подстановку:
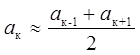 ,
,
тогда
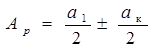 , (5)
, (5)
где (-) при к – четном,
(+) при к – нечетном.
II. ЧАСТНЫЕ СЛУЧАИ ДИФРАКЦИИ ФРЕНЕЛЯ
2.1. Недиафрагмированный волновой фронт
Если 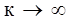 , (экрана с диафрагмой нет), то амплитуда результирующего колебания в точке Р равна:
, (экрана с диафрагмой нет), то амплитуда результирующего колебания в точке Р равна:
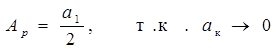 ,
,
а волны, дошедшие до точки Р от остальных участков волновой поверхности, погасили друг друга.
Итак, можно сделать вывод: в результате интерференции вторичных волн в точке Р будут наблюдаться только волны, приходящие из очень малой части волновой поверхности, расположенной около прямой, соединяющей точку S - источник волн с точкой Р, т.е. в однородной и изотропной среде волны будут распространятся прямолинейно при безграничном фронте волны.
Подтвердим этот вывод расчетами.
Найдем выражение для радиуса зоны Френеля.
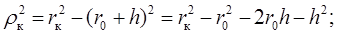
для малой диафрагмы можно считать, что h2 ® 0.
Зная, что 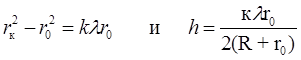 ,
,
получим
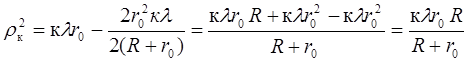 , (6)
, (6)
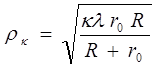
Оценим размеры первой зоны Френеля (к = 1).
Пусть  ,
,
тогда ;
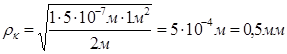
Как видно, размеры первой зоны соответствуют предположению о том, что в точку Р приходят волны от малой части волнового фронта, т.е., свет распространяется по прямой SP.
2.2. Дифракция на круглом отверстии
Пусть свет распространяется от источника S к экрану В, на пути которого стоит экран D с круглым отверстием (рис. 4).
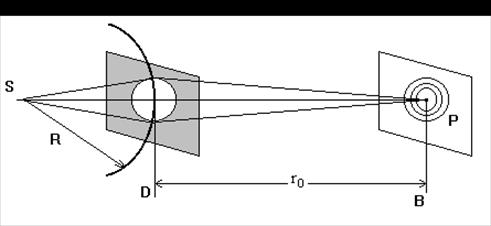
Рис. 4
Зная, что 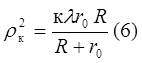 , найдем общее число зон, которое укладывается в отверстии:
, найдем общее число зон, которое укладывается в отверстии:
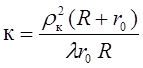 (7)
(7)
Из (7) видно, что число зон, укладывающихся в отверстии, не есть постоянная величина. При постоянных 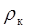 и R число зон зависит от r, т.е. от расстояния от диафрагмы до точки наблюдения. Таким образом, при движении наблюдателя из точки Р вдоль прямой SP число зон будет меняться, а, следовательно, будет происходить в точке Р чередование света и тени.
и R число зон зависит от r, т.е. от расстояния от диафрагмы до точки наблюдения. Таким образом, при движении наблюдателя из точки Р вдоль прямой SP число зон будет меняться, а, следовательно, будет происходить в точке Р чередование света и тени.
Если в отверстии экрана будет укладываться нечетное число зон Френеля, то в точке Р будет свет. Наибольшая интенсивность света в точке Р будет тогда, когда в отверстии укладывается только одна зона Френеля. Покажем это.
Если к = 1, то 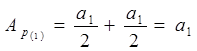 .
.
Если к = 51, то 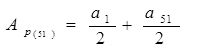 . Так как
. Так как 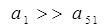 , то
, то
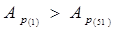 .
.
Если в отверстии экрана будет укладыватьсячетное число зон Френеля, то в точке Р будет происходитьгашение волн. Наименьшая интенсивность света в точке Р будет в том случае, когда в отверстии укладывается только две зоныФренеля.
Покажем это.
Если к = 2, то 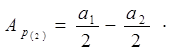 Так как
Так как 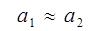 , то
, то 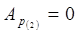 , т.е.- гашение полное.
, т.е.- гашение полное.
Если к = 50, то 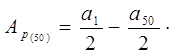 Так как
Так как 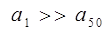 , то
, то 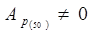 , т.е. - гашение не полное.
, т.е. - гашение не полное.
2.3. Дифракция на круглом непрозрачном экране
Если на пути света от точечного источника S поставить непрозрачный экран D, то область геометрической тени на экране будет ограничена окружностью с центром в точке Р и радиусом РВ. С другой стороны, за счет дифракции точка Р окажется освещенной, т.к. совокупное действие световых волн, исходящих от незаслоненной экраном D части волновой поверхности, сведется к амплитуде от первой открытой зоны (рис. 5).
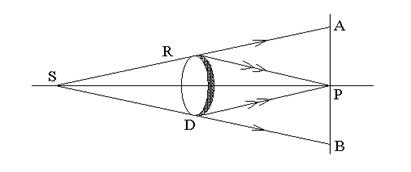
Рис. 5
Пусть экран закрывает на волновом фронте m-зон. Остальная часть фронта безгранично открыта, тогда свет в точку Р придет от первой открытой (m+1) зоны. Покажем это.
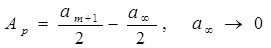 , т.е.
, т.е. 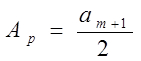 .
.
Таким образом, в точке Р всегда будет свет. Интенсивность его будет тем больше, чем меньше зон закрывает непрозрачный экран, т.к. 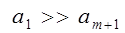 .
.
В лабораторных опытах явление дифракции наблюдается только при прохождении света через препятствия малых размеров. Однако, при увеличении расстояний между предметом и местом наблюдения можно обнаружить дифракционные явления и на предметах сравнительно большего размера.
ОПИСАНИЕ УСТАНОВКИ И ЕЕ НАСТРОЙКА 1
Эксперимент проводится на учебном приборе ЭСФЭ-1 «Оптика», состоящем из лазерного блока и блоков линз.
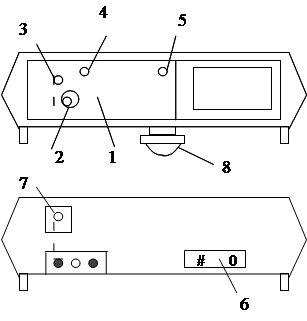 |
На рис. 6 изображены лицевая и задняя панели прибора.
 Рис. 6
Рис. 6
1) корпус блока лазерного излучения;
2) механическая ось;
3) выходное отверстие лазерного излучения;
4) ручка управления заслонкой;
5) индикатор;
6) клемма заземления;
7) кнопка включения питания;
1 Перед выполнением работы изучите инструкцию к прибору ЭСФЭ – 1, правила техники безопасности.
1. Убедитесь, что риска на ручке (4) установлена против черной точки. В этом положении заслонка перекрывает выходное окно (3), через которое лазерное излучение выходит наружу.
Перед выполнением работы изучите инструкцию к прибору ЭСФЭ-1, правила техники безопасности.
2. Нажмите кнопку (7) на задней стенке блока лазерного излучателя. При этом на передней панели должна загореться индикаторная лампа (5).
3. Откройте выходное окно, установив ручку (4) против красной точки. На дальнем непрозрачном экране должно появиться яркое красное пятно.
| В н и м а н и е !!! Всегда смотреть вдоль луча. Никогда нельзя смотреть навстречу лучу! |
4. Для наблюдения дифракции по Френелю, лазерный пучок делается расходящимся с помощью рассеивающей линзы 2 (рис. 7). Чтобы ввести линзу, на механической оси 2 (рис. 6) блок линз (Л) нужно поставить в положение "-11". Это означает, что в приборе встроена отрицательная линза с фокусным расстоянием 11 мм. Остальные два блока должны иметь положения D(III), D(º).
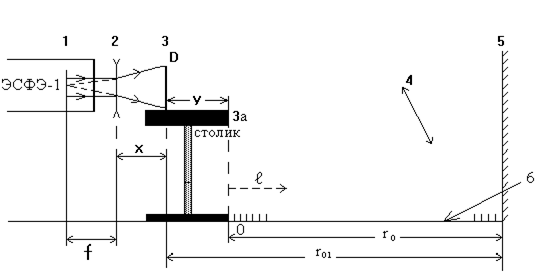 |
5. Для наблюдения дифракции на простых объектах соберите установку (рис. 7),
Рис. 7
в которую, кроме прибора ЭСФЭ-1 (1) с линзой (2), входят: подвижный столик (3а), на котором устанавливаются простые объекты в держателе (3):
а) диафрагма с малым круглым отверстием [2-9];
б) диафрагма с круглыми непрозрачными экранами [2-8];
в) диафрагма с тонкими нитями [2-7].
Кроме того, в установке используется собирающая линза (F=163 мм), укрепленная на штативе (4); экран (5); линейка с делениями (6).
6. Hа самом близком расстоянии от линзы (2) установите столик 3а и поставьте на столик держатель с диафрагмой [2-9] с самым малым круглым отверстие, получите на экране (5) дифракционную картину. Близко от экрана поставьте собирающую линзу (4). Расстояние х надо подобрать такое, чтобы в центре картины был четкий максимум или минимум, а не промежуточное состояние. Для удобства настройки на четкую картину max или min используйте собирающую линзу (4), как лупу. Измерьте это расстояние и запишите над табл.1.
Дата добавления: 2015-04-29; просмотров: 1001;
